Злобная математическая задачка

Вы наверняка встречали задачки, подобные этой, основанные на внимательности и знании хотя последовательности выполнений действий из школьной арифметики. Ответ под катом.

Часто они сопровождаются чем нибудь типа "95% студентов математического факультета не могут решить этой задачки!"

Но вот, что интересно. Иногда математика становится настоящим садистом. Вот - блестящий пример:

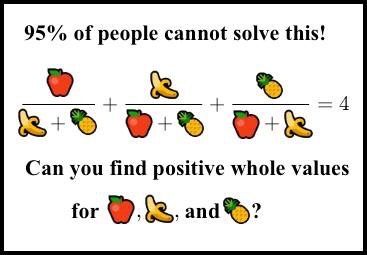
...или, в математической форме, a/(b+c) + b/(a+c) + c/(a+b)=4

Задачку надо решить в целых положительных числах. Если предположить, что возможны отрицательные, она решается относительно просто.

Но она решается и в положительных целых числах!  Только 99,97% людей её не решат. Ни перебором, ни с помощью компа. Это диофантовы уравнения, а они могут иметь... э-э...

Короче, наименьшее решение столь невинно выглядящего уравнения:

земляничка=154476802108746166441951315019919837485664325669565431700026634898253202035277999,
бананчик=36875131794129999827197811565225474825492979968971970996283137471637224634055579,
ананасик=4373612677928697257861252602371390152816537558161613618621437993378423467772036

И это даёт действительно 4!

Полученные числа 80-ти разрядные. А вот если заменить четвёрку в правой части на 178, то вместо 80 разрядов в ответах понадобится 398 605 460 разрядов, то есть ответы станут в пять миллионов раз длиннее. А если вместо 4 встанет число 896, ответ будет иметь триллионы разрядов.

Решение про собачек: 15