У истоков линейной алгебры

ЛИНЕЙНАЯ АЛГЕБРА, раздел алгебры, изучающий векторные (линейные) пространства и их подпространства, линейные отображения (операторы), линейные, билинейные и квадратичные функции (функционалы или формы) на векторных пространствах.
Исторически первым разделом линейной алгебры была теория систем линейных уравнений. В связи с изучением этих систем появились понятия матрицы и определителя.
Первые элементы линейной алгебры такие, как решения линейных уравнений и такие арифметические приёмы, как тройное правило и правило ложного ппредположения, были сформулированы ещё в древности.

В "Началах" Евклида рассматриваются две теории "линейного" характера: теория величин и теория целых чисел. Близкие к современным матричным методам подходы к решению систем линейных уравнений обнаруживаются у вавилонян (системы из двух уравнений с двумя переменными) и древних китайцев (в "Математике в девяти книгах", до трёх уравнений с тремя переменными).
Однако даже в конце XVIII -- начале XIX века считалось, что системы линейных уравнений с числом переменных, большим количества уравнений или с линейно-зависимыми коэффициентами в левой части попросту некорректны.


Линейная алгебра-- раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения, системы линейных уравнений, среди основных инструментов, используемых в линейной алгебре -- определители, матрицы, сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры.
Линейная алгебра обобщена средствами общей алгебры, в частности, современное определение линейного (векторного) пространства опирается исключительно на абстрактные структуры, а многие результаты линейной алгебры обобщены на произвольные модули над кольцом. Более того, методы линейной алгебры широко используются и в других разделах общей алгебры, в частности, нередко применяется такой приём, как сведение абстрактных структур к линейным и изучение их относительно простыми и хорошо проработанными средствами линейной алгебры, так, например, реализуется в теории представлений групп. Функциональный анализ возник как применение методов математического

анализа и линейной алгебры к бесконечномерным линейным пространствам, и во многом базируется на методах линейной алгебры и в дальнейших своих обобщениях. Также линейная алгебра нашла широкое применение в многочисленных приложениях (в том числе, в линейном программировании, в эконометрике) и естественных науках (например, в квантовой механике).

Методы, сформировавшие линейную алгебру как самостоятельный раздел математики, уходят корнями в другие разделы. Ферма в 1630-е годы, создав классификацию плоских кривых, ввёл в математику (ключевой для линейной алгебры) принцип размерности и разделил задачи аналитической геометрии по числу неизвестных (с одним неизвестным -- отыскание точки, с двумя -- кривой или геометрического места на плоскости, с тремя -- поверхности). Эйлер создал классификацию кривых по порядкам обратив внимание на линейный характер преобразований координат, ввёл в оборот понятие аффинного преобразования (и само слово "аффинность").




Первое введение понятия определителя для целей решения систем линейных уравнений относят к Лейбницу (1678 или 1693 год), но эти работы не были опубликованы. Также определитель обнаруживается в трудах Сэки Такакадзу 1683 года, в которых он обобщил метод решения систем линейных уравнений из древнекитайской "Математики в девяти книгах" до уравнений с неизвестными. Маклорен, фактически используя простейшие определители в трактате вышедшем 1748 году приводит решения систем их двух линейных уравнений с двумя неизвестными и трёх уравнений с тремя неизвестными. Крамер и Безу в работах по проблеме отыскания плоской кривой, проходящей через заданную точку, вновь построили это понятие (правило Крамера сформулировано в 1750 году), Вандермонд и Лагранж дали индуктивное определение для случаев, а целостное определение и окончательные свойства определителей дали Коши (1815) и Якоби (1840-е годы). Гауссу (около 1800 года) принадлежит формализация метода последовательного исключения переменных для решения этих задач, ставшего известным под его именем (хотя по существу для решения систем линейных уравнений именно этот метод и использовался с древности).
Понятие матрицы ввёл Сильвестр в 1850 году. Кэли обстоятельно разрабатывает матричное исчисление, публикуя в 1858 году "Мемуары о теории матриц", принципиально, что Кэли рассматривает матрицы как нотацию для линейных подстановок. Системы линейных уравнений в матрично-векторном виде впервые появились, по-видимому, в работах Лагера (1867).

Основной базой линейной алгебры стало фактически влившееся в раздел векторное исчисление, очерченное Гауссом в работах по геометрической интерпретации комплексных чисел (1831) и обретшее окончательную форму в трудах Мёбиуса, Грассмана и Гамильтона 1840-х -- 1850-х годах. Так, Гамильтон в 1843 году обобщает комплексные числа докватернионов и даёт им геометрическую интерпретацию по аналогии с гауссовой (Гамильтону, в том числе, принадлежит и введение термина "вектор"), а в 1844 году Грассман строит понятие внешней алгебры, описывающей подпространства линейного пространства. Всеобщее признание векторного исчисления в конце XIX века существенно связано с применением векторов ведущими физиками-теоретиками того времени, прежде всего, Максвеллом, Гиббсом, Хевисайдом, в частности, физиками тщательно проработана векторная алгебра в трёхмерном евклидовом пространстве.

Начиная с этого времени векторы проникают и в школьные программы.
В 1888 году Пеано на базе исчисления Грассмана впервые в явном виде сформулировал аксиомы линейного пространства (векторных пространств над полем действительных чисел в том числе бесконечномерных) и применил обозначения, сохранившиеся в употреблении в XX--XXI века.

Аксиоматическое определение векторного и евклидова пространства было впервые чётко сформулировано в начале XX века практически одновременно Вейлем и фон Нейманом, исходя из запросов квантовой механики.

Габриель Крамер (Gabriel Cramer), один из создателей линейной алгебры, родился 31 июля 1704 года в Женеве, в семье французского врача. С раннего возраста проявил большие способности в области математики. В 18 лет защитил диссертацию, в двадцатилетнем возрасте выставил свою кандидатуру на вакантную должность преподавателя на кафедре философии Женевского университета.

Кандидатур было три, все произвели хорошее впечатление, и магистрат принял соломоново решение: учредить отдельную кафедру математики и направить на неё Крамера и ещё одного претендента с правом путешествовать за свой счёт.
Крамер воспользовался этим правом и два года путешествовал по Европе. В Базеле он познакомился и подружился с Иоганном Бернулли и Эйлером, в Лондоне – с Галлеем и де Муавром, в Париже – с Мопертюи и Клеро. По возвращении он поддерживал с ними переписку.
В 1728 г. Крамер находит решение Санкт-Петербургского парадокса, близкое к тому, которое 10 годами спустя публикует Даниил Бернулли.

Парадокс Санкт-Петербурга или лотерея Санкт-Петербурга - это парадокс, связанный с игрой в подбрасывание монетки, когда ожидаемый выигрыш в теоретической игре в лотерею приближается к бесконечности, но, тем не менее, кажется, что для участников он составляет лишь очень небольшую сумму.
Парадокс Санкт-Петербурга - это ситуация, когда наивный критерий принятия решения, учитывающий только ожидаемую ценность, предсказывает курс действий, который, предположительно, ни один реальный человек не был бы готов предпринять. Было предложено несколько решений этого парадокса.

Проблема была изобретена Николасом Бернулли, который изложил её в письме к Пьеру Раймону де Монморту 9 сентября 1713 года. Однако парадокс получил своё название от анализа, проведенного двоюродным братом Николаса Даниэлем Бернулли, одно время проживавшим в Санкт-Петербурге, который в 1738 году опубликовал свои мысли об этой проблеме в Комментариях Императорской академии наук Санкт-Петербурга.
В 1729 году Крамер возвращается в Женеву и возобновляет преподавательскую работу. Он участвует в конкурсе, объявленном Парижской Академией, задание в котором: есть ли связь между эллипсоидной формой большинства планет и смещением их афелиев? Работа Крамера занимает второе место (первый приз получил Иоганн Бернулли).

Около 1740 года Иоганн Бернулли поручает Крамеру хлопоты по изданию сборника собрания своих трудов. В 1742 году Крамер публикует сборник в 4 томах, а вскоре (1744) выпускает аналогичный (посмертный) сборник работ Якоба Бернулли и двухтомник переписки Лейбница с Иоганном Бернулли. Все эти издания имели огромный резонанс в
научном мире.

В 1742 г. Крамер обобщил на случай трёх произвольных точек поставленную ещё Паппом (вторая половина третьего века) задачу о вписании в круг треугольника, стороны которого проходят через три точки, лежащие на одной прямой. В геометрии известен парадокс Крамера или парадокс Крамера–Эйлера - утверждение о том, что число точек пересечения двух кривых высшего порядка на плоскости может быть больше числа произвольных точек, которые обычно необходимы для определения одной такой кривой.
Во время второго путешествия в Париж (1747) Крамер познакомился с Даламбером.

Самая известная из работ Крамера – изданный незадолго до кончины трактат „Введение в анализ алгебраических кривых", опубликованный в 1750 г. на французском языке. В нём впервые доказывается, что алгебраическая кривая n -го порядка в общем случае полностью определяется заданием точек.
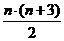
Для доказательства Крамер строит систему линейных уравнений и решает её с помощью алгоритма, получившего позже название „метод Крамера".

Решение систем линейных уравнений Крамер представил в виде столбца дробей с общим знаменателем – определителем матрицы.
Термина „определитель" (детерминант) тогда ещё не существовало (его ввёл К.Ф.Гаусс в 1801г.), но Крамер дал точный алгоритм его вычисления. Метод Крамера сразу же получил дальнейшее развитие в трудах Безу, Вандермонда и Кэли, которые завершили создание основ линейной алгебры.

Теория определителей быстро нашла множество приложений в астрономии и механике (вековое уравнение), при решении алгебраических систем и т.д.
Крамер провёл классификацию алгебраических кривых до пятого порядка включительно.
В 1751 г. он получил серьёзную травму после дорожного инцидента с каретой. Доктор рекомендует ему отдохнуть на французском курорте, но там его состояние ухудшается, и 4 января 1752 года Крамер умирает в Баньоль-сюр-Сез, Франция.
