ОСНОВАТЕЛЬ МАТЕМАТИКИ НОВОГО ВРЕМЕНИ

Среди пионеров борьбы за строгость и чистоту математики, рядом с именами Гаусса, Вейерштрасса, Чебышёва и его учеников Ляпунова и Маркова, девизом которых была «строгость, строгость и строгость», называют имя выдающегося французского учёного Огюстена Луи Коши, великого труженика, по продуктивности сравнимого разве что с Эйлером.
Огюстен-Луи Коши (Augustin Louis Cauchy) родился 21 августа 1789г., через несколько недель после штурма Бастилии, в Париже. Его отец, Луи-Франсуа, был юристом, глубоко верующим католиком, убежденным монархистом и воспитал у сына эти убеждения. Он вместе со своей женой, Марией-МадаленойДезестр, он спасся бегством из Парижа во время террора. Огюстен-Луи был первым из шести их детей. В семье царила атмосфера дружбы и уважения. На всю жизнь Огюстен сохранил сыновнюю почтительность к отцу и сердечную нежность к матери. Даже в зрелые годы он обращался за советом к матери. Всю жизнь он придерживался крайних антиреволюционных и пророялистских взглядов.
Во время Великой Французской революции семья Коши переселилась в свое небольшое имение в Аркюэйле, по соседству с которым были имения французского математика, физика и астронома Пьера Симона Лапласа и французского химика Клода Луи Бертолле. Эти ученые, а также Ж. Лагранж, часто посещавший П. Лапласа, оказали большое влияние на О.Коши. Они заметили математическую одаренность Коши.
Первым учителем Огюстена был отец, который занимался со своими сыновьями историей и древними языками, заставляя их читать античных авторов в подлиннике.
В 1801г. Лагранж сказал, что этот мальчик в скором времени затмит всех геометров, но посоветовал отцу не показывать ему до 17 лет книги по математике.

Благодаря основательному домашнему образованию у Коши выработалось сочетание математического гения с замечательным писательским талантом. Коши сочинял стихи, и даже некоторые факты математики и астрономии изложил в стихах.
Когда к власти пришёл Наполеон, отец вернулся на правительственную службу и семья вернулась в Париж. В 1802 г. Огюстен поступил в Центральную школу в Париже, где изучал главным образом древние языки. В 1805 г. сдал вступительный экзамен в Центральную школу общественных наук Пантеона (переименованную впоследствии в Политехническую школу) вторым по списку.Политехническую школу он окончил через два года. Во время учебы в Политехнической школе он с большим успехом изучал математику.
Политехническая школа была организована в 1794 г. по предложению группы учёных и инженеров во главе с создателем начертательной геометрии, французским математиком и инженером Гаспаром Монжем, в связи с тем, что Франции, находившейся в то время в состоянии войны с европейской коалицией, были очень нужны инженеры. Школа представляла собой военное учебное заведение нового типа, в котором основное внимание уделялось изучению фундаментальных наук: математики, механики, физики и химии. Этим предметам посвящались первые два года и только на третьем году изучались специальные технические дисциплины. Однако вскоре третий год обучения был отменен, и выпускники Политехнической школы поступали в специальные учебные заведения: Школу инженеров, Артиллерийскую школу, Горную школу, Школу мостов и дорог. Таким образом, Политехническая школа стала чем-то вроде общетехнического факультета для технических высших учебных заведений страны.

Вскоре после основания Политехнической школы в ней начали преподавать такие знаменитые математики и механики, как Г. Монж, Жан Батист Жозеф Фурье, Ж. Лагранж, Гаспар Клэр Франсуа Мари Риш Прони, С. Пуассон. Кроме лекций, учебные планы предусматривали проведение упражнений по решению задач и лабораторных работ по физике и химии, которые впервые были включены в учебные планы.
После окончания Политехнической школы Коши первым по списку поступил в 1807 г. в Школу мостов и дорог, которую окончил в 1810 г., заняв первое место также и на выпускных экзаменах. После окончания школы Коши, в звании кандидата на должность инженера работал на постройке Урского канала, а затем на сооружении моста в Сен-Клу. В 1810 г. уехал в Шербур, где в 21 год начал самостоятельную инженерную работу в Шербурском порту.
Свободное от работы время в Шербуре он посвящал математическим исследованиям и уже в 1811—1812 гг. представил несколько мемуаров в Парижскую академию наук.
К этому времени относится его знаменитое исследование о многогранниках. Первым значительным результатом Коши в математике было доказательство теоремы, что любой выпуклый многогранник неизгибаем. (В 1977 году Коннелли нашёл невыпуклый многогранник, который не был неизгибаем.)

В 1812 году Коши доказал гипотезу Ферма, что всякое целое число – это сумма самое большее n n-угольных чисел.
Три года Коши работал военным инженером в Шербуре, участвуя в строительстве военно-морской базы, а в 1813г. переехал в Париж и целиком занялся научной и преподавательской работой в Политехнической школе, Сорбонне и Коллеже де Франс.
В 1816г. Коши стал профессором математики в Политехнической школе. Интенсивная научная работа послужила основанием для баллотировки О.Коши в Парижскую академию наук: в первый раз в 1813 г. и второй в 1814 г., но оба раза он потерпел неудачу. Только в 1816 г., когда из состава Академии по политическим мотивам были выведены: математик, механик, военный инженер и государственный деятель Лазар НиколлаМаргерит Карно и Г. Монж, О. Коши королевским декретом был назначен на место Г.Монжа.Гаспар Монж, морской министр первой французской республики, организатор её обороны, с возвращением Бурбонов на трон он потерял всё: был лишён всех титулов и наград, изгнан из Академии наук и вынужден был скрываться от властей.
У свидетелей этого белого террора реставрации, естественно, возникал вопрос: кто займет место Монжа в академии? Найдется ли во Франции математик, настолько лишённый чувства приличия, чтобы занять место чистейшего и добрейшего гражданина, крупнейшего учёного, создателя Политехнической школы, воспитавшей десятки учёных с мировым именем?..
Такой человек нашёлся. Это был выпускник этой школы ученик Монжа Огюстен Луи Коши, проявивший себя как ярый монархист. И тут нечему удивляться: Коши был не избран в Парижскую академию, а назначен властями.

Потому и сетуя по поводу столь жёстких репрессивных мер, применённых к республиканцу Монжу, в те времена с возмущением говорили: «Его место беззастенчиво занял Коши — великий учёный, не наделённый, однако, совестью. Он был преступно невнимателен к молодым учёным, терял их работы. Он — соучастник, одна из причин гибели Галуа и Абеля».
Примечателен и другой факт, характеризующий Коши несколько иначе. Потому и умолчать о нём нельзя. В 1822 году Михаила Васильевича Остроградского посадили в парижскую долговую тюрьму по требованию хозяина гостиницы, которому он сильно задолжал. Пребывая в тюрьме, Остроградский написал мемуар по теории волн в сосуде цилиндрической формы и послал его на рассмотрение Коши. Тот не отверг работу и не затерял её, а одобрил и добился опубликования в Трудах Парижской академии наук. Более того, он выкупил Михаила Васильевича из тюрьмы, не будучи уже очень богатым, и порекомендовал его на должность преподавателя в лицее. А, казалось бы, странным: убеждённый клерикал выручил бывшего студента Харьковского университета, лишённого диплома за вольнодумство и непосещение лекций по богословию. Было ли это проявлением неосведомленности Коши в вопросах политических взглядов русского математика, трудно сказать. Достоверно известно лишь одно: в 1831 году Огюстен Луи Коши стал почётным иностранным членом Петербургской академии наук, тогда как другого французского математика и философа-просветителя маркиза Кондорсе, активно участвовавшего в Великой французской революции (на первом её этапе), по велению Екатерины II из академии исключили.

Коши был лектором по призванию, мастером слова и интересным рассказчиком. Огромное значение для совершенствования преподавания имели его лекционные курсы по алгебраическому анализу, по исчислению бесконечно малых, по приложению анализа к геометрии.
4 апреля 1818 года Огюстен Луи женился на Алоизе де Бюре – близкой родственнице основного издателя его работ. В 1819 году у них родилась первая дочь, Мария Француаза Алисия, а в 1823 году – вторая, Мария Матильда.
Коши стал одним из основоположников современного строгого изложения анализа, свободного от неоправданных ссылок на интуицию. В своих работах Коши дал определение непрерывности функции, пределу, непрерывности, производной, дифференциалу, интегралу, сходимости ряда и т. д., провёл исследование свойств элементарных функций, разработал учение об условной и абсолютной сходимости рядов, дал определение интеграла, дал новый подход к проблеме разложения функций в ряды и т.д.Его определение непрерывности опиралось на понятие бесконечно малого, которому он придал новый смысл: у Коши бесконечно малое — переменная величина, стремящаяся к нулю. Ввёл понятие радиуса сходимости ряда.
В 1826-1828 годах им были написаны "Лекции о приложении анализа к геометрии". В этих курсах Коши дал определение непрерывности функции, построил строгую теорию сходящихся рядов, ввел определенный интеграл как предел интегральных сумм. Вся система анализа построена на базе предела. Книги Коши долгое время служили образцом для курса анализа.

Коши написал более 800 работ, которые занимают 27 томов его собрания сочинений. Его работы относятся к различным областям математики (преимущественно к математическому анализу) и математической физики.
В 1830году, после свержения династии Бурбонов, королём стал Луи-Филлип Орлеанский, что, с точки зрения Коши, было катастрофой.От Коши потребовали присягнуть на верность новому правительству. Он отказался это сделать, и был немедленно уволен со всех должностей. Коши решает покинуть Францию: покинув свою семью, он последовал за Карлом X Бурбоном в изгнание.
Сначала он жил в Швейцарии, потом два года в Турине, где король Сардинии создал для него кафедру теоретической физики. В 1833 г. Карл Х пригласил Коши для образования герцога Бордосского (графа Шамбора), с которым Коши несколько лет путешествовал по Европе. В награду он получил титул барона.
В 1834 году в Прагу приезжает жена и дочери Огюстена Луи. Семья вновь воссоединилась после четырёх лет разлуки.
Многократно ему предлагали различные учёные должности, но он от них отказывался, не желая принимать присягу.

В 1838 г. Коши возвращается во Францию. По отношению к нему было сделано исключение: ему разрешили преподавать в иезуитском колледже без присяги, и вернули все прежние титулы. Прошло ещё 10 лет, прежде чем он получил одну из своих прежних кафедр (ранее у него были кафедры в Сорбонне и в Колледж де Франс) – революция отменила присягу на верность. Он вернулся в Сорбонну. Наполеон III оставил его в этой должности в 1852 году.
Характер у Коши был сложный. Он ревностно относился к защите своих авторских прав, спорил о приоритете даже по мелким вопросам. Высокообразованный, вежливый и доброжелательный, он вместе с тем небрежно относился к молодым учёным. Широко известен случай, когда он в своих бумагах затерял одну из лучших работ молодого норвежского математика Н.Х.Абеля. Только благодаря настойчивости немецкого математика К.Г.Якоби Коши разыскал эту работу. Но произошло это уже после смерти Абеля.
А вот другое описание, имеющееся в литературе, этого эпизода. Многие соотечественники жестоко осуждали его политическую и гражданскую позицию, из-за чего ученый часто поддавался критике и даже откровенным наговорам. Так, однажды, его обвинили в утере работ талантливых математиков того времени – Нильса Хенрика Абеля и Эвариста Галуа. Якобы, из-за халатности Коши, они погибли, так и не дождавшись признания своих трудов. На самом деле, учёный вряд ли получал хоть одну работу от Галуа, поскольку тот не считал академика авторитетным учёным. Что же касается Абеля, то профессор, если и терял его рукописи, то быстро снова их нашёл, и даже оставил положительный отзыв.
Не известно, терял ли рукописи Абеля академик Коши, но есть сведения, что он их быстро нашёл и дал хвалебный отзыв, когда Нильс Хенрик Абель уже умер. Что же касается истинного сына революции гениального математика и республиканца Галуа, то хорошо известно, что на его работы Коши не дал ответа. И нет ничего удивительного в том, что в последнем, предсмертном письме другу перед трагической дуэлью Эварист Галуа просил: «Ты публично попросишь Якоби или Гаусса дать заключение не о справедливости, а о значении этих теорем. После этого, я надеюсь, найдутся люди, которые сочтут нужным расшифровать всю эту галиматью». Как видим, он не внёс Коши в число немногих авторитетов в математике, которым бы мог довериться.
Чтобы характеристика Коши и его отношения к другим учёным, и не только молодым, не показалась предвзятой, приведём ещё один эпизод. Речь идёт об ученике и последователе Монжа, выдающемся геометре и механике Жане Викторе Понселе. Будучи офицером инженерных войск Наполеона, вместе с 26 тысячами французов он попал в плен к русским. И там, в плену, в далеком от европейских научных центров Саратове, написал семь тетрадей, которые по возвращении в Париж превратились в ныне знаменитый «Трактат о проективных свойствах фигур», где были обстоятельно изложены принципы новой науки — проективной геометрии и впервые сформулирован принцип двойственности.
Но его работы, посланные в Академию наук в 1824 году, не встретили того приёма, какого он ожидал. Коши в своих докладах ставил «новую геометрию», как называл её Понселе, ниже анализа. Понселе, надолго сохранивший об этой неудаче неприятное воспоминание, отдался почти исключительно изучению механики и в этой новой области он замечательно преуспел.
Коши ненавидел прогрессивную философию 18-го века. При выборах в Академию наук Коши руководствовался не научными заслугами кандидата, а близостью его политических и религиозных взглядов.
Заслугой Коши является собрание и уточнение богатого наследия математиков 18-го столетия.
В работах по оптике Коши дал математическую разработку теории Френеля и теории дисперсии.
Были периоды, когда Коши каждую неделю представлял в Парижскую Академию наук новый мемуар. Академик А.Н. Крылов по этому поводу отмечает: «Коши писал такое множество работ, как превосходных, так и торопливых, что ни Парижская академия, ни тогдашние математические журналы их вместить не могли, и он основал свой собственный математический журнал, в котором помещал только свои работы». К. Гаусс про наиболее торопливые его работы выразился так: «Коши страдает математическим поносом». Неизвестно, не говорил ли Коши в отместку, что «Гаусс страдает математическим запором».
Быстрота, с которой он переходил от одного предмета к другому, дали ему возможность проложить в математике множество новых путей. Большой заслугой Коши является то, что он развил основы теории аналитических функций комплексного переменного, заложенные в 18-ом веке Л.Эйлером и Ж.Даламбером. О продуктивности Коши-математика свидетельствует целый ряд терминов, определений и понятий, вошедших в науку, таких, как признак Коши, критерий Коши, задачи Коши, интеграл Коши, уравнения Коши–Римана и Коши–Ковалевской, относящиеся к разным разделам математического анализа, математической физики, теории чисел, и других дисциплин.

Его биограф аббат Муано писал: "Коши был роста выше среднего, тонок и очень строен. Походка была скорая; так как он дорожил временем и не желал терять минуты, ему часто приходилось бегать. Его волосы и брови были редки, что придавало ему вид несколько юный. Лоб его был высокий и очень открытый, глаза немного томные с несколько блуждающим взглядом, но полные жизни и ума. Нос его длинный тонкий, губы открытые, голос сильный и не совсем обыкновенный, произношение его парижское и до крайности картавое, цвет лица бледный и немного болезненный; будучи на вид слабый, он редко болел''.
Коши писал: «Я христианин, то есть верую в Божество Иисуса Христа, как и Тихо де Браге, Коперник, Декарт, Ньютон, Ферма, Лейбниц, Паскаль, Гримальди, Эйлер и другие, как все великие астрономы, физики и математики прошлых веков.… Во всём этом христианском вероучении я ничего не вижу, что сбивало бы с толку мою голову, было бы ей вредно. Напротив, без этого святого дара веры, без знания о том, чего мне надеяться и что ожидает меня в будущем, душа моя в неуверенности и беспокойстве металась бы от одной вещи к другой, и эта тревога души и неуверенность в мыслях есть то, что нередко производит отвращение к жизни и может, в конце концов, повести к самоубийству.»
Коши был способным публицистом. Его "Курс алгебраического анализа" (1821), "Резюме лекций по исчислению бесконечно малых" (1823), "Лекции по приложениям анализа к геометрии" (1826-1828) служили образцом для большинства курсов позднейшего времени. Поток его математических статей не прекращался до самой смерти.
Коши был членом Лондонского королевского общества и почти всех академий наук. С его именем в математике связаны понятия: вычет,задача Коши,интегральная формула Коши,интегральная теорема Коши,неравенство Коши — Буняковского,неравенство между средним арифметическим и средним геометрическим,теорема Больцано — Коши,теорема Коши в теории групп,теорема Коши о среднем значении,распределение Коши,условия Коши — Римана,функциональное уравнение Коши, теорема Коши – Ковалевской, теорема Коши – Адамара.
Он был кавалером ордена Почетного легиона. Многие из его открытий используют и по сей день в математических дисциплинах.
В 4 часа утра, в ночь на 23 мая 1857 года, в возрасте 67 лет Огюстен Луи Коши умер. Похоронен в местечке Ссо, где была школа, находившаяся на его попечении.
Его имя внесено в список величайших учёных Франции, помещённый на первом этаже Эйфелевой башни. В 1935 г. Международный астрономический союз присвоил имя О. Л. Коши кратеру на видимой стороне Луны.
Имя учёного присвоено многим научным теоремам и понятиям.
Задача Коши
Доказать, что для любого натурального значения n выполняется неравенство
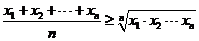
, где х1, х2, ∙∙∙, хn – положительные числа, причём равенство достигается лишь в случае х1=х2=∙∙∙=хn.
Однажды он сказал:
Сначала необходимо изучить факты, умножить число наблюдений, а затем искать формулы, которые их связывают, чтобы таким образом различать конкретные законы, регулирующие определенный класс явлений. В общем, это не так. до тех пор, пока эти конкретные законы не будут установлены, можно ожидать, что они обнаружат и сформулируют более общие законы, которые дополняют теории, объединяя множество по-видимому очень разнообразных явлений вместе в рамках единого управляющего принципа.
Я никогда не выставлю напоказ то маленькое знание, которое я получил благодаря заботе и помощи, оказанной мне отцом. Если я чему-то научился, то только потому, что он позаботился о том, чтобы научить меня. Если бы он не взял на себя труд наставляя меня, я был бы таким же невежественным, как и многие другие дети .
Остатки возникают ... естественно, в нескольких областях анализа ... Их рассмотрение обеспечивает простые и удобные в использовании методы, которые применимы к большому количеству разнообразных вопросов и некоторым новым результатам ...
