Выдающийся математик средневековья

Леонардо Пизанский (Фибоначчи) (Leonardo Pisano Fibonacci)родился около 1170 года в Пизе (Италия). Его отец был купцом и государственным вельможей, представителем нового класса предпринимателей.
Fibonacci, или filius Bonacci, означает сын Боначчи, а слово "bonacci" означает "добродушный". Отец Фибоначчи по торговым делам часто бывал в Алжире. Тогда Пиза была одним из крупнейших коммерческих средоточий, активно сотрудничавших с исламским Востоком. Отец Фибоначчи энергично торговал в одной из факторий, основанных итальянцами на северном побережье Африки. Благодаря этому ему удалось "устроить" своего сына, будущего великого математика Фибоначчи, в одну из арабских школ, где он и смог получить превосходное для того времени математическое образование. Начальное образование Леонардо получил в Бугие (Алжир) под руководством местного учителя. Он овладел арифметикой и алгеброй арабов. В последующие годы он посетил многие страны Европы и Востока (Египет, Сирию, Византию, Сицилию) и всюду пополнял свои знания по математике. Леонардо изучал труды математиков стран мусульманского вероучения (таких как ал-Хорезми); по арабским переводам он ознакомился также с достижениями античных и индийских математиков.

Еще до Крестовых походов арабское воздействие проникло на Запад. Тем не менее, наибольшее проникновение арабской культуры на Запад началось после Крестовых походов, которые обессилили арабский народ, но с другой стороны усилили арабское воздействие на христианский Запад. Не только хлопок и сахар Палестины, перец и чёрное дерево Египта, самоцветные камни и пряности Индии ищет и ценит христианский Запад в арабском мире. Он начинает разбираться в том культурном наследстве "великого античного Востока", хранителем которого стала арабская культура. Открывшийся мир не мог не ослеплять своими красками и научными достижениями – и всё обширнее становится в западном обществе спрос на арабские географические карты, учебники алгебры и астрономии, арабское зодчество.

Фридрих II, император (с 1220 года) Священной Римской империи, воспитанный в традициях южной Италии, был внутренне глубоко далёк от европейского христианского рыцарства. Cтоль любимые его дедом рыцарские турниры Фридрих II совсем не признавал. Вместо этого он культивировал гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами. На таких турнирах и заблистал талант Леонардо Фибоначчи. Этому способствовало хорошее образование, которое дал сыну купец Боначчи, взявший, как говорилось, его с собой на Восток и приставивший к нему арабских учителей. Покровительство Фридриха стимулировало выпуск научных трактатов Фибоначчи: "Kниги абака", "Практической геометрии" (1220г.), "Kниги квадратов" (1225г.). По этим книгам, превосходящим по своему уровню арабские и средневековые европейские сочинения, учили математику чуть ли не до времен Декарта
( XVII в.).
В 1202 году Фибоначчи написал "Книгу абака" ("Liber abaci", в дополненном и переработанном виде она вышла в 1228 г.). Под «абаком» Леонардо понимал не счётную доску, а арифметику.
Этот объемный труд, насчитывающий в печатном варианте 459 страниц, стал настоящей энциклопедией математических знаний того времени и сыграл важную роль в их распространении в странах Западной Европы в следующие несколько столетий. Работа написана на латыни и считается первым сочинением такого рода, автор которого был христианином.

До нашего времени дошла лишь рукопись, датированная 1228 годом.
В этой книге вводятся индийские цифры и нуль, излагаются наиболее практические методы вычислений с целыми и дробными числами, приведены способы извлечения квадратных и кубических корней. Здесь же содержатся правило пропорционального деления, тройное правило, цепное правило, способ определения пробы металлов. Неизвестное у него обозначается словом "вещь", отрезок он обозначает или двумя буквами, как это делают и теперь, или одной буквой, поставленной в начале отрезка.

«Книга абака» совершила переворот в позиционной системе исчисления, поскольку в нём автор представил миру совершенно новую и наиболее приемлемую систему расчётов. Ранее для математических действий применялась римская нотация, но в сравнении с новой методикой Фибоначчи она явно проигрывала. В своей работе Леонардо описал варианты использования индийских цифр, которые ранее были менее изучены, и представил примеры решения задач, касающихся торговли. В эпоху Возрождения позиционная система Фибоначчи стала повсеместно известной.
Книга Леонардо содержит также сведения по алгебре и учение о пропорциях в том виде, как это изложено у аль - Хорезми. Он не признавал отрицательных корней при решении квадратных уравнений.
В этой книге Леонардо первый в Европе стал применять алгебру для решения геометрических вопросов.
В предисловии к "Книге абака" он писал: "Я решился, присоединив к индийскому методу кое-что от себя, кое-что от тонкостей геометрического искусства Евклида, составить труд, который я теперь обнародую в 15 отделах, дабы род латинян не оставался более несведущим во всех этих вещах".

Первые пять глав книги посвящены арифметике целых чисел на основе десятичной нумерации. В VI и VII главе Леонардо излагает действия над обыкновенными дробями. В VIII–X книгах изложены приёмы решения задач коммерческой арифметики, основанные на пропорциях. В XI главе рассмотрены задачи на смешение. В XII главе приводятся задачи на суммирование рядов — арифметической и геометрической прогрессий, ряда квадратов и, впервые в истории математики, возвратного ряда. В XIII главе излагается правило двух ложных положений и ряд других задач, приводимых к линейным уравнениям. В XIV главе Леонардо на числовых примерах разъясняет способы приближённого извлечения квадратного и кубического корней. Наконец, в XV главе собран ряд задач на применение теоремы Пифагора и большое число примеров на квадратные уравнения.

«Книга абака» резко возвышается над европейской арифметико-алгебраической литературой XII–XIV вв. разнообразием и силой методов, богатством задач, доказательностью изложения. Последующие математики широко черпали из неё как задачи, так и приёмы их решения.
Леонардо Пизанский впервые:
сформулировал правило для нахождения суммы членов произвольной арифметической прогрессии;
рассмотрел возвратную последовательность, в которой каждое число, начиная с третьего, равно сумме двух предшествующих ему чисел;

ввёл термин «частное» для обозначения результата деления;
описал способ приведения дробей к общему знаменателю с помощью нахождения наименьшего общего кратного знаменателей (более рациональный, чем использовали арабские математики).
Кроме того, Фибоначчи самостоятельно разработал ряд алгебраических приемов решения задач, исследовал некоторые уравнения высших степеней, сводящиеся к квадратным, и первым среди европейских ученых подошёл к введению отрицательных чисел и их толкованию как долга, что по тем временам являлось огромным достижением.
Некоторые из затронутых в труде Фибоначчи вопросов в разное время привлекали внимание ученых-математиков и не раз упоминались в более поздних сочинениях.

Уровень сочинения оказался столь высок, что осилить и воспользоваться изложенными в нём сведениями смогли главным образом учёные-математики, отчасти современники Леонардо, и в ещё большой мере – представители последующих поколений.Фактически лишь спустя три столетия после выхода в свет «Liber abaci» стало заметно её влияние на работы других авторов. С появлением труда Фибоначчи европейские ученые эпохи Средневековья, бывшие зачастую философами-схоластами или духовными лицами, для кого математика не была основным занятием, стали уделять больше внимания алгебре и затрагивать в своих исследованиях её новые вопросы. Однако первых серьезных результатов удалось достичь только в эпоху Возрождения, к началу XVI столетия, когда группа итальянских математиков (Сципион дель Ферро, Никколо Тарталья, Джероламо Кардано, Людовико Феррари) получила общее решение кубических уравнений, положив тем самым начало высшей алгебре. Как ученый Фибоначчи не только превзошел, но и на столетия опередил западноевропейских математиков своего времени.

В 1220 г. он написал "Практическую геометрию", в которой, пользуясь трудами Евклида и других греческих авторов, излагает вопросы об определении площадей плоских прямолинейных фигур, об измерении круга, о многоугольниках, о сфере и цилиндре. Леонардо принадлежат и собственные открытия. Из них наиболее известным является числовая последовательность, называемая числами Фибоначчи.
Одной из задач в "Книге абака" была следующая задача, решение которой связано с числовой последовательностью 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, и т.д.: "Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения". Леонардо нашёл ответ - 377.
Указанные выше числа (числа Фибоначчи) имеют красивые геометрические применения, важные приложения в биологии (явление филотаксиса) и во многих других задачах. Последовательность Фибоначчи имеет весьма любопытные особенности:
Сумма любых двух соседних чисел равна следующему числу в последовательности. Например: 3 + 5 = 8; 5 + 8 = 13 и т.д.
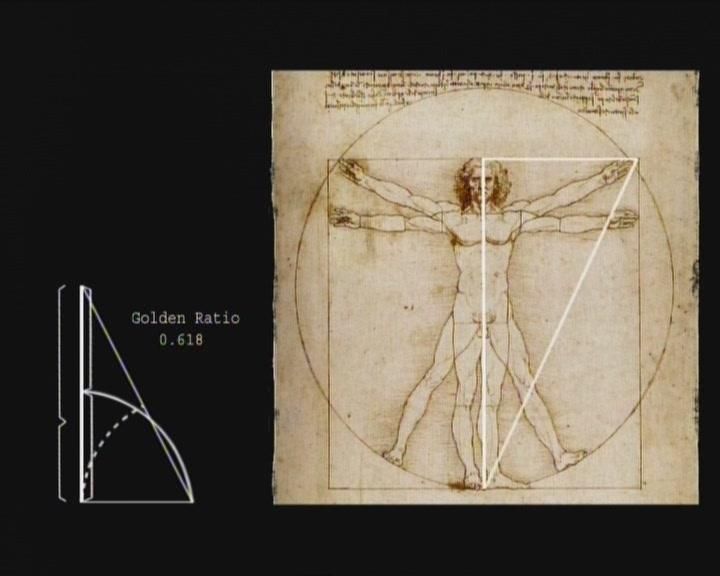
Отношение любого числа последовательности к следующему приближается к 0,618 (после первых четырех чисел). Например: 1: 1 = 1; 1: 2 = 0,5; 2: 3 = 0,67; 3: 5 = 0,6; 5: 8 = 0,625; 8: 13 = 0,615; 13: 21 = 0,619 и т.д. Обратите внимание, как значение соотношений колеблется вокруг величины 0,618, причём размах флуктуаций постепенно сужается; а также на величины: 1,00; 0,5; 0,67.

Отношение любого числа к предыдущему приблизительно равно 1,618 (величина обратная 0,618). Например: 13: 8 = 1,625; 21: 13 = 1,615; 34: 21 = 1,619. Чем выше числа, тем более они приближаются к величине 0,618 и 1,618.
Отношение любого числа к следующему за ним через одно приближается к 0,382, а к предшествующему через одно - 2,618. Например: 13: 34 = 0,382; 34: 13 = 2,615.
Последовательность Фибоначчи содержит и другие любопытные соотношения, но те, которые здесь приведены - самые важные и известные.

В 19 веке ученые заметили, что цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках и т. д. "упакованы" по двойным спиралям, завивающимся навстречу друг другу. При этом числа "правых" и "левых" спиралей всегда относятся друг к другу, как соседние числа Фибоначчи (13:8, 21:13, 34:21, 55:34). Многочисленные примеры двойных спиралей, встречающихся повсюду в природе, всегда соответствуют этому правилу. Гёте называл спираль "кривой жизни".
Раковины улиток подчиняются последовательности Фибоначчи. Широко известным примером последовательности Фибоначчи являются сосновые шишки. Все шишки растут по спирали, начиная с основания, где была ножка, далее круговыми движениями по краям, пока не достигнут верхнего конца.

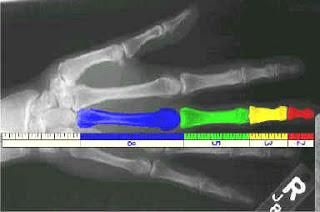
Другой примечательный пример - тело человека. В теле человека отношение длины предплечья к длине руки равно 1.618, т.е. “золотому сечению”. Другими широко известными примерами в теле человека являются: 1. Отношение между длиной и шириной лица. 2. Отношение расстояния между губами и местом где сходятся брови к длине носа. 3. Отношение размера рта к ширине носа. 4. Отношение расстояния между линией плеч и верхом головы к длине головы. 5. Отношение расстояния между пупком и коленями к расстоянию между коленями и ступням. 6. Отношение расстояния между кончиками пальцев и локтем к расстоянию между запястьем и локтем. Та же последовательность существует у листьев тополя, вишни, яблони, сливы, дуба и липы. Молекула ДНК закручена двойной спиралью.
Замечательным является проявление последовательности Фибоначчи и в строении растений. Такой вывод можно сделать, наблюдая за ростом и развитием стеблей и цветов sneezewort'а. Каждая его новая ветвь, прорастая, дает начало другим.
На самом деле Фибоначчи не является первооткрывателем своей последовательности. Дело в том, что коэффициент 1,618 или 0,618 был известен еще древнегреческим и древнеегипетским математикам, которые называли его "золотым коэффициентом" или "золотым сечением". Его следы мы находим в музыке, изобразительном искусстве, архитектуре и биологии. Греки использовали принцип "золотого сечения" при строительстве Парфенона, египтяне - Великой пирамиды в Гизе. Свойства "золотого коэффициента" были хорошо известны Пифагору, Платону и Леонардо да Винчи. Эта закономерность в математике интересовала ещё одного учёного средневековья – Фому Аквинского. Движимый желанием «алгеброй гармонию измерить», учёный сделал вывод о прямой связи математики и красоты. Эстетические чувства, возникающие при созерцании гармоничных, пропорционально созданных природой объектов, Фома Аквинский объяснял тем же принципом, что и Фибоначчи. Средневековый математик Лука Пачоли назвал это соотношение (φ=1,618) Божественной пропорцией. Кеплеpом эта последовательность названа "одним из сокровищ геометрии".
Фибоначчи привёл первое доказательство того, что три медианы треугольника пересекаются в одной точке (Архимеду этот факт был известен, но его доказательство до нас не дошло, если оно и существовало).
В трактатах „Цветок" и „Книга квадратов" (1225г.) исследуется кубическое уравнение х3+2х2+10х=20, предложенное Фибоначчи на математическом состязании при дворе императора Фридриха II и решается несколько неопределённых квадратных уравнений (например, в одной из задач требовалось найти рациональное квадратное число, которое, будучи увеличено или уменьшено на 5, вновь даёт рациональные квадратные числа).
Его труды получили распространение только в конце 15 века, когда итальянский математик Лука Пачоли (1454-1514) переработал их и опубликовал в 1494 г. в своей книге "Сумма".
Со словом "средневековье" в нашем сознании ассоциируется разгул инквизиции, костры, на каковых сжигали ведьм и еретиков, крестовые походы за "телом господним". Наука в те поры явно не была приоритетом. В этих условиях появление книги по математике "Liber abaci" Леонардо Пизано Фибоначчи, стало важным событием в научной жизни общества.

По сегодняшний день ничего не известно о внешности учёного. Прижизненных портретов математика не осталось, а те, что имеются, представляют собой современное представление о Леонардо. Наследие Фибоначчи насчитывает несколько научных работ, биографических данных он после себя не оставил. Не установлено, был ли он женат, имел ли семью, детей - история не сохранила этих сведений, достоверно известна лишь дата его смерти - 1250 год. Предполагают, что, возможно, он пал во время одного из Крестовых походов, сопровождая императора Фридриха Гогенштауфена. Почти на тысячу лет он был забыт, а сейчас его идеи - в центре огромного множества исследований.

Подобно Пифагору, привнёсшему в греческую науку знания, некогда полученные от египетских и вавилонских жрецов, Фибоначчи во многом способствовал передаче приобретенных им в молодости математических знаний индусов и арабов в западноевропейскую науку и заложил фундамент для её дальнейшего развития.
Хотя он и был величайшим математиком средневековья, единственные памятники Фибоначчи - это статуя напротив Пизанской башни (в 1978 г.перенесён на кладбище), установленный в XΙX веке, и две улицы, которые носят его имя, одна - в Пизе, а другая - во Флоренции. Имя математика носит научная ассоциация в Италии и издаваемый ею научный журнал. Именем Фибоначчи назван один из астероидов Солнечной системы. В честь Фибоначчи названы следующие объекты математики и естествознания: числа Фибоначчи; тождество Брахмагупты – Фибоначчи; система исчисления Фибоначчи; кубы Фибоначчи; многочлены Фибоначчи; фибоначиева куча; метод поиска Фибоначчи; треугольник Фибоначчи – Хосоя; слова Фибоначчи; фибоначиевы алгоритмы; посвящённый числам Фибоначчи проект Евросоюза в сфере образования.
Таким образом, имя Фибоначчи не забыто потомками, его вклад в науку неоценим.
Задачи Леонардо Пизанского
Вот несколько задач из «Liber abaci»:
Найти число, 19/20 которого равны квадрату самого числа.
Семь старух отправляются в Рим. У каждой по семь мулов, каждый мул несёт по семь мешков, в каждом мешке по семь хлебов, в каждом хлебе по семь ножей, каждый нож в семи ножнах. Сколько всего предметов?
Эта задача обошла много стран, первое известное упоминание о ней было ещё в Древнем Египте в папирусе Ахмеса. (Ответ: 137 256).
Один говорит другому: "Дай мне 7 динариев, и я буду в 5 раз богаче тебя". А другой говорит: "Дай мне 5 динариев, и я буду в 7 раз богаче тебя". Сколько у каждого?
Некто купил 30 птиц за 30 монет. Из числа этих птиц за каждых 3 воробьёв заплачено 1 монета, за каждые 2 горлицы - также 1 монета и, наконец, за каждого голубя - по 2 монеты. Сколько было птиц каждой породы?
Предположим, что моя корова, которая впервые телится на второй год своей жизни, приносит ежегодно по телочке. Каждая тёлочка, как и её мать, будет телиться ежегодно, начиная со второго года от рождения, и каждый, раз будут рождаться тёлочки. Сколько коров родят моя корова и её потомки за 25 лет?
Задача о выборе наилучшей системы гирь для взвешивания на рычажных весах впервые была сформулирована именно Фибоначчи. Леонардо Пизанский предлагает два варианта задачи:
а) Простой вариант: требуется найти пять гирь, с помощью которых можно найти все веса меньше 30, при этом гири можно класть только на одну чашу весов (Ответ: 1, 2, 4, 8, 16). Решение строится в двоичной системе счисления.
б) Сложный вариант: требуется найти наименьшее число гирь, с помощью которого можно взвесить все веса меньше заданного (Ответ: 1, 3, 9, 27, 81,…). Решение строится в системе счисления по основанию три.
- Кроме задачи о кроликах, Фибоначчи предлагал ряд других задач по теории чисел:
а) Найти число, которое делится на 7 и даёт в остатке единицу при делении на 2, 3, 4, 5 и 6; (Ответ: 301)
б) Найти число, произведение которого с семёркой даёт остатки 1, 2, 3, 4, 5 при делении на 2, 3, 4, 5, 6, соответственно;
в) Найти квадратное число (то есть число, равное квадрату целого числа), которое при увеличении или уменьшении на 5 давало бы квадратное число.
- Сплав из 30 весовых частей состоит из трёх металлов: первый металл достоинством по три монеты на одну часть, второй металл по две монеты на одну часть, а у третьего металла каждые две части стоят по одной монете; стоимость всего сплава 30 монет. Сколько частей каждого металла содержит сплав? (Ответ: 3 части первого металла, 5 частей второго металла, 22 части третьего). В таких терминах Фибоначчи переформулировал задачу о птицах.
Рассказывают, что…
Сам математик никогда не называл себя «Фибоначчи». Это прозвище он получил позднее. По некоторым данным, так итальянского математика прозвал Гийом Либри в 1838 году. Одна из версий гласит, что слово «Фибоначчи» является сокращением названия «Книги абака». По другой версии, это слово обозначает «сын Боначчи», потому что сам Леонардо иногда подписывал свои работы как Боначчи. Иногда он использовал также имя Леонардо Биголло — слово bigollo на тосканском наречии значило «странник», а также «бездельник».
Талант итальянского математика заинтересовал императора Фридриха II, и вместе с ним и его придворных. В 1225 году самодержец подал идею - позвать талантливого итальянца во дворец на турнир по математике. Хорошо образованный мужчина понравился правителю и впоследствии получил императорское покровительство. Следующие годы он проживал и занимался изучением чисел в резиденции правителя.
Фибоначчи много времени проводил на турнирах по математике при дворе императора и особое внимание уделял задачам, они же занимали почётное место в его сочинениях. В своих работах он собрал всевозможные математические и алгебраические задачи, решения и дополнения к ним. Задачи для турниров выбирал он сам, иногда это делал его соперник - философ императора Иоганн Палермский. Эти задачи, или аналогичные им ещё долго можно было встретить в произведениях других математиков.
В том же 1225 году учёный написал труд «Книга квадратов», посвятив его диофантовым уравнениям второй степени, и благодаря ему приблизился к славе великих математиков, таких как Диофант и Ферма. В 1240 году Леонардо удостоился денежного вознаграждения за заслуги перед городом, в котором всю жизнь трудился на ниве науки.
К работам Фибоначчи, дошедшим до наших дней, относится сочинение «Цветок». Оно датировано 1225 годом и является результатом исследования математиком кубического уравнения. Идею подобного рода уравнения ему предложил Иоанн Палермский, но существует гипотеза, что последний заимствовал её у Омара Хайяма.
«Liber abaci» содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной. Само изложение было словесным, лишенным привычных для современного читателя символов и формул, а решение примеров и задач, носивших, как мы говорим сегодня, частный характер, сводилось к описанию действий, которые следовало применить в той или иной конкретной ситуации, и нередко сопровождалось разъяснениями или полезными комментариями автора.
Благодаря Фибоначчи европейцы познакомились с общими правилами решения квадратных уравнений, описанными в трактате аль-Хорезми.
Золотое сечение – деление целого (например, отрезка) на такие части, которые соотносятся по следующему принципу: большая часть относится к меньшей так же, как и вся величина (например, сумма двух отрезков) к большей части.
Первое упоминание о золотом сечении можно встретить у Евклида в его трактате «Начала» (примерно 300 лет до н.э.). В контексте построения правильного прямоугольника.
Привычный нам термин в 1835 году ввёл в оборот немецкий математик Мартин Ом.
Если описывать золотое сечение приблизительно, оно представляет собой пропорциональное деление на две неравных части: примерно 62% и 38%. В числовом выражении золотое сечение представляет собой число 1,6180339887.
Золотое сечение находит практическое применение в изобразительном искусстве (картины Леонардо да Винчи и других живописцев Ренессанса), архитектуре, кинематографе («Броненосец «Потемкин» С. Эзенштейна) и других областях. Долгое время считалось, что золотое сечение – наиболее эстетичная пропорция. Такое мнение популярно и сегодня. Хотя по результатам исследований визуально большинство людей не воспринимают такую пропорцию наиболее удачным вариантом и считают слишком вытянутой (непропорциональной).
23 ноября отмечается как день Фибоначчи, потому что, когда дата написана в формате mm / dd (11/23), цифры в дате образуют последовательность Фибоначчи: 1,1,2,3.
Первая тысяча знаков значения отношения числа из ряда Фибоначчи к предыдущему числу для больших чисел равно 1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
