Опередивший время

В плеяде великих математиков XIX века одним из самых известных является ирландец сэр Уильям Роуэн Гамильтон. Сделанные им открытия в физике и математике были прорывными для своего времени и послужили фундаментом для дальнейшего развития науки на многие десятилетия вперед.
Уильям Роуэн Гамильтон (William Rowan Hamilton) был величайшим математиком из всех, когда-либо рождённых в Ирландии. Он появился на свет, когда часы отбивали полночь с 3 на 4 августа 1805 года, и впоследствии так и не смог окончательно решить, какой же из дней считать днём своего рождения. По большей части он склонялся к 3-му, но на его надгробии указана дата «4 августа», потому что ближе к концу жизни он перешёл на эту дату.
Гамильтон родился в Дублине. Он был четвёртым из девяти детей в семье ирландки Сары Хаттон и полуирландца, полушотландца Арчибальда Гамильтона. Арчибальд работал в Дублине юристом. Из-за финансовых затруднений и плохого здоровья родителей было решено с годовалого возраста передать мальчика на воспитание дяде по отцу. Дядя, Джеймс Гамильтон, человек хорошо образованный, служил викарием и учителем в городе Трим; он с симпатией отнёсся к племяннику и всячески помогал его развитию. Вскоре Уильям окончательно остался без родителей — мать умерла, когда мальчику было 12 лет, отец пережил её на два года. Позднее Гамильтон взял на себя заботу о трёх своих осиротевших сёстрах.

Уже в детстве мальчик проявил необыкновенные дарования. В 7 лет он знал древнееврейский язык; в 12 — под руководством дяди Джеймса, хорошего лингвиста, знал уже 12 языков и среди них персидский, арабский и санскрит. В 13 лет он написал руководство по сирийской грамматике.
Двумя годами раньше Гамильтону попался латинский перевод «Начал» Евклида, и он детально изучил это сочинение; в 13 лет он прочёл «Универсальную арифметику» Ньютона; в 16 лет — большую часть «Математических начал натуральной философии» Ньютона, в 17 лет — начал изучение «Небесной механики» Лапласа.
В 1815—1823 годах Уильям учился в школе, затем 18-летний юноша поступил в Тринити-колледж Дублинского университета. Там он показал столь блестящие способности (первый по всем предметам), что в 1827 году, ещё 22-летним студентом, по рекомендации ушедшего в отставку Бринкли был назначен на его место — профессором астрономии в Дублинском университете и королевским астрономом Ирландии. Этот пост он занимал 38 лет.
Гамильтон опубликовал ряд работ по геометрической оптике, представляющих большую ценность для теории оптических инструментов, но чисто астрономическими проблемами занимался мало; комиссии из Лондона дважды подвергали его критике за недостаточное усердие.

В университете бывший студент Гамильтон, так никогда и не защитивший диссертацию, читал курс небесной механики.
В 1833 году Гамильтон женился на Хелен Бэйли. У них родились два сына и дочь. Брак оказался не слишком удачным, и Гамильтон начал злоупотреблять алкоголем.
Гамильтон жил и думал в атмосфере поэзии, он писал поэмы по любому случаю и на любую тему. Естественно, что, будучи разочарован (причём дважды) в любви, он изливал свое горе в стихах, писал послания ко дню рождения своих сестёр, сонеты о красоте местности. Но, поняв, что его истинной поэзией была математика, он переключился на научное поприще.
В период 1834—1835 годов появились классические работы по «гамильтоновой механике». Шотландский математик Питер Тэт назвал эти работы «крупнейшим дополнением теоретической динамики со времени великих эпох Ньютона и Лагранжа». За открытия в оптике и по совокупности научных заслуг вице-король Ирландии возвёл Гамильтона в рыцарское достоинство баронета (1835) и назначил ежегодное пособие в 200 фунтов, а лондонское Королевское общество наградило его (совместно с Фарадеем) Королевской медалью.

В том же 1835 году Гамильтон завершил разработку нового, чрезвычайно общего подхода к решению задач динамики в виде вариационного принципа (принцип Гамильтона). Спустя почти столетие именно этот подход оказался ключевым для создания квантовой механики, а открытый Гамильтоном вариационный принцип с успехом был использован при разработке уравнений поля общей теории относительности.
В 1837 году Гамильтона избрали президентом Ирландской королевской академии. В том же году по представлению академиков В. Я. Буняковского, М. В. Остроградского и П. Н. Фусса он был избран членом-корреспондентом Петербургской академии наук за работу «Об общем методе в динамике».
Его сочинения носят печать гениальности, и можно сказать, что он далеко опередил своих современников.

1843 год стал в жизни Гамильтона переломным. В этом году он открыл алгебраическую систему кватернионов — обобщение системы комплексных чисел — и оставшиеся два десятилетия своей жизни посвятил их исследованию. В Великобритании теорию кватернионов встретили с необыкновенным энтузиазмом и «глубоким уважением, доходящим до благоговения»; в Ирландии (а затем — и в Англии) она стала обязательным элементом образования.
В 1846 году случился неприятный скандал на обеде Геологической ассоциации, куда Гамильтон явился в состоянии чрезвычайно сильного опьянения. В результате он подал в отставку с поста президента Ирландской академии.
Год спустя скончался дядя Джеймс, заменивший Уильяму отца.
Он выставил себя таким полным дураком на научном обеде в Дублине, что после этого зарёкся пить и в течение последующих двух лет пил только воду. Однако когда астроном Джордж Эйри начал посмеиваться по поводу его воздержания, Гамильтон принялся в ответ поглощать алкоголь в усиленных количествах. С того времени он стал хроническим алкоголиком.

Его жизнь становилась всё более и более беспорядочной; после его смерти, последовавшей 2 сентября 1865 года (как полагали, от подагры, которой часто страдают тяжёлые пьяницы), его математические статьи были найдены вперемешку с мусором и объедками. Похоронен он на дублинском кладбище.
Согласно историку математики Э.Т. Беллу, глубочайшей трагедией Гамильтона были не алкоголь и не неудачный брак, а его упрямая вера в то, что кватернионы содержат в себе ключ к математике и физике Вселенной.
Свой многолетний труд, монографию «Элементы кватернионов», он успел завершить за несколько дней до смерти.
Первая из его замечательных работ была представлена в 1823 году доктору Бринклею, его предшественнику по кафедре, потом, после больших дополнений и разъяснений, напечатана в 1828 году в журнале. После там же появились три дополнения к этой статье, в третьем из которых было теоретически доказано, что двупреломляющие кристаллы с двумя оптическими осями должны обладать коническим лучепреломлением по направлениям осей. Эксперимент в Тринити-колледже подтвердил это предсказание.

Его мемуар 1834—1835 годов заключает в себе самые важные открытия по механике и теории интегрирования систем дифференциальных уравнений, развитые потом Якоби. Этот же мемуар указал возможность получения дифференциальных уравнений движения, исходя из нового принципа, названного принципом Гамильтона, являющегося развитием принципа наименьшего действия, установленного ранее Мопертюи, Эйлером и Лагранжем. Созданная им гамильтонова динамика оказалась в XX веке фундаментом теории микромира.
Гамильтону же принадлежит введение в механику особого наглядного приёма изображения изменений величин и направлений скорости точки, совершающей какое-либо прямо— или криволинейное движение.
В 1837 году им разработана аксиоматическая теория комплексных чисел как пар вещественных.
В 1840-е годы английская школа математиков упорно пыталась найти расширение поля комплексных чисел с несколькими мнимыми единицами. Только много позже было доказано, что такое расширение не может быть полем — оно либо некоммутативно, либо неассоциативно, либо содержит делители нуля. Первым добился успеха Гамильтон — открыл кватернионы, некоммутативную числовую структуру с тремя мнимыми единицами (1843).
Геометрическая интерпретация комплексных чисел открывала возможность плодотворного применения их в планиметрии и при решении двумерных задач математической физики.

Пытаясь добиться аналогичного результата в пространственном случае, Гамильтон в течение нескольких лет работал над обобщением понятия комплексного числа и созданием полноценной системы «чисел» из троек действительных чисел (сложение должно было — как и для комплексных чисел — быть покомпонентным; проблема состояла в надлежащем определении умножения).
Не преуспев в этом, он обратился к четвёркам действительных чисел. Озарение пришло к нему в один из октябрьских дней 1843 года — во время прогулки по дублинскому мосту; так появились кватернионы.
Наряду с представлением кватернионов четвёрками действительных чисел он — по аналогии с комплексными числами — записывал кватернионы и как формальные суммы вида q = a + bi + cj + dk, где i, j и k — три кватернионные единицы (аналоги мнимой единицы i). В дальнейшем многие годы Гамильтон посвятил подробному исследованию новых чисел и их практическим приложениям, написав на эту тему 109 статей и две объёмные монографии «Лекции о кватернионах» и «Элементы кватернионов».

В 1853 году вышел труд Гамильтона «Лекции о кватернионах». Интересно отметить, что операцию умножения кватернионов, установление которой ему долгое время не давалось, он открыл неожиданно на ходу, когда шёл на работу. Об этом факте он писал своему сыну: «...16 октября 1843 года, оказавшегося понедельником и днём заседания Ирландской академии, когда я шёл в академию, чтобы председательствовать, по набережной королевского канала в сопровождении твоей матери, и, несмотря на её разговор со мной, мои мысли так чётко работали в подсознании, что дали, наконец, результат, важность которого я тотчас же ощутил. Казалось, замкнулась электрическая цепь и вспыхнула искра, пришёл вестник многих долгих лет неуклонной работы и мысли».

В 1878 году Г. Фробениус объяснил причину неуспеха Гамильтона с тройками действительных чисел, доказав следующее утверждение (теорема Фробениуса): над полем действительных чисел Ў существуют лишь три конечномерные ассоциативные алгебры с делением: само Ў, поле комплексных чисел J и тело кватернионов H.
Крупнейшим продолжателем работ Гамильтона и популяризатором кватернионов стал его ученик — шотландский математик Питер Тэт, предложивший для них множество приложений к геометрии, сферической тригонометрии и физике.
В ходе исследований Гамильтон попутно ввёл понятие векторного поля и создал основы векторного анализа. Он открыл векторное произведение, предложил оператор «набла». На основе работ Гамильтона Гиббс и Хевисайд завершили систему векторного анализа.
Геометрия обязана Гамильтону и такими терминами, как «коллинеарность» и «компланарность» (применявшимися только к точкам; для векторов с общим началом в соответствующих случаях употреблялись выражения termino-collinear и termino-coplanar).
Феликс Клейн высказал мнение, что «кватернионы хороши и применимы на своём месте, но они не имеют всё же такого значения, какое имеют обыкновенные комплексные числа». Во многих областях применения были найдены более общие и практичные средства, чем кватернионы. Например, в наши дни для исследования движений в пространстве чаще всего применяется матричное исчисление.

Но исторический вклад кватернионов в развитие математики был неоценим. Анри Пуанкаре писал: «Их появление дало мощный толчок развитию алгебры; исходя от них, наука пошла по пути обобщения понятия числа, придя к концепциям матрицы и линейного оператора, пронизывающим современную математику. Это была революция в арифметике, подобная той, которую сделал Лобачевский в геометрии».
Оба главных открытия Гамильтона — новая формулировка механики и кватернионы — сыграли существенную роль в XX веке при возникновении квантовой механики.
Он был глубоко верующим человеком и даже избирался окружным церковным старостой. Среди его работ есть два труда посвящённых религиозной теме.
Гамильтон живо интересовался философией и особенно ценил Беркли и Канта. Он не верил, что открытые нами законы природы адекватно отражают реальные закономерности. В соответствии с Кантом, Гамильтон считал научные представления порождениями человеческой интуиции.
В 1856 году Гамильтон исследовал группу симметрий икосаэдра и показал, что у неё имеются три порождающих элемента.
В 1859г. сэр Уильям Гамильтон придумал игру–головоломку. Основой её был правильный додекаэдр, сделанный из дерева. Каждая вершина этого додекаэдра была помечена названием одного из крупных городов (Брюссель, Франкфурт, Дели и т.д.). Задача состояла в нахождении пути вдоль ребер додекаэдра, проходящего через каждый город в точности по одному разу.
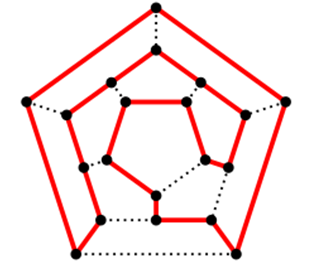
Сопоставляя додекаэдру его граф, ту же задачу можно переформулировать так: найти на графе замкнутый путь, проходящий через все вершины графа (или покрывающий все вершины графа). Такой путь называется гамильтоновым циклом, а графы, в которых он имеется, называются гамильтоновыми. Если путь, покрывающий все вершины графа, не замкнут, то граф называется полугамильтоновым.
Эта игра, красочно оформленная как «Путешествие вокруг света», долгое время выпускалась в разных странах Европы.
В 1861 г. Гамильтон в области планиметрии доказал носящую его имя теорему Гамильтона: Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
Несколько работ Гамильтона посвящены уточнению работ Абеля по разрешимости уравнения пятой степени и численным методам. В ходе своих исследований кватернионов Гамильтон доказал ряд алгебраических теорем, которые в наши дни относят к теории матриц. Важную в линейной алгебре теорему Гамильтона — Кэли он фактически доказал для матриц размерности
4х4, само понятие матрицы и формулировку теоремы (без доказательства) опубликовал Кэли (1858), для общего случая доказательство дал Фробениус в 1898 году.
Продолжатель его работ Якоби называл Гамильтона «Лагранжем этой страны».
Как собственные блестящие способности, так и неудачная личная жизнь вызвали в Гамильтоне непреодолимое увлечение творческим научным трудом. Он работал по 12 и более часов в день, забывая о еде. Как-то составил себе шутливую эпитафию: «Я был трудолюбивый и правдолюбивый».

Множество понятий и утверждений в науке связано с именем У. Р. Гамильтона: оператор Гамильтона; Гамильтона–Якоби уравнение; гамильтониан (квантовая механика); Гамильтонов граф; Гамильтонова механика; параметры Родрига — Гамильтона; принцип Гамильтона; теорема Гамильтона — Кэли; уравнение Гамильтона — Якоби — Беллмана; уравнения Гамильтона; функция Гамильтона.
В честь учёного назван кратер Гамильтон на видимой стороне Луны. В Ирландии два научных института названы в честь величайшего математика страны: Гамильтоновский институт при Национальном университете Мейнут и Гамильтоновский институт математики при дублинском Тринити-колледжеhttp://wikiredia.ru/wiki/%D0%93%D0%B0%D0%BC%D0%B8%D0%BB%D1%8C%D1%82%D0%BE%D0%BD_%D0%A3._%D0%A0. - cite_note-100. В 2005 году научная общественность многих стран отметила 200-летие Уильяма Гамильтона; правительство Ирландии объявило этот год «годом Гамильтона», а Центральный банк Ирландии выпустил памятную монету достоинством 10 евро.

Рассказывают, что…
*Академик А. Н. Крылов писал, что Гамильтон — «один из величайших математиков, отличавшийся многочисленностью своих работ, важностью заключавшихся в них открытий, глубиною мысли, оригинальностью методов, вместе с тем и как вычислитель, имевший мало себе равных».
* История показала, что Гамильтон трагически обманывал себя, когда продолжал утверждать о роли кватернионов: «Я по-прежнему определенно заявляю, что это открытие представляется мне настолько же важным для середины девятнадцатого столетия, насколько открытие флюксонов было важным для семнадцатого столетия.» Никогда ещё великий математик столь отчаянно не ошибался.
*Кватернионы возникают при попытке расширить комплексные числа за счет увеличения размерности (оставляя её, тем не менее, конечной) с сохранением при этом максимально возможного числа законов алгебры. Законы, которые мы хотим оставить, это обычные свойства сложения и вычитания, большая часть свойств умножения и возможность деления на все, кроме нуля. На этот раз жертву приходится приносить более серьезную; это-то и доставило Гамильтону столько терзаний. Надо выкинуть закон коммутативности умножения.
В 1898 году Адольф Гурвиц доказал, что система кватернионов единственна. Кватернионы являются единственной конечномерной алгеброй с делением, которая содержит вещественные числа и не совпадает с вещественными или комплексными числами.
