„НЕ ТРОНЬ МОИХ ЧЕРТЕЖЕЙ”

О жизни Архимеда (ок. 287-212г. до н.э.) отрывочные сведения дошли до нас благодаря Титу Ливию, Цицерону, Плутарху, Витрувию. Они жили на много лет позже описываемых событий, и достоверность этих сведений оценить трудно.
Архимед (др.-греч. Ἀρχιμήδης) родился в городе Сиракузы, что был расположен на восточном побережье острова Сицилия и на тот момент являлся греческой колонией. Отец будущего учёного, математик и придворный астроном по имени Фидий, с детства привил сыну любовь к науке. Гиерон, который впоследствии стал правителем Сиракуз, приходился близким родственником семейству, так что мальчику обеспечили прекрасное образование. Его детство пришлось на тот период, когда царь Пирр вёл войны с карфагенянами и римлянами, пытаясь создать греческое государство нового образца. Особо отличился в этой войне Гиерон.

Архимеду домашней подготовки оказалось достаточно, чтобы с ранних лет он мог проявить свои гениальные способности. Некоторое время Архимед учился в знаменитой Александ¬ри, которая была в то время научным центром. Здесь Птолемеями, правителями Египта, были собраны лучшие греческие учёные и мыслители того времени. Также в Александрии находилась самая большая в мире библиотека. Там он изучал творения Демокрита, греческого философа, и Евдокса, знаменитого механика, астронома, математика и врача. В процессе обучения будущий учёный завёл дружбу с Эратосфеном, главой Александрийской библиотеки, и Кононом, древнегреческим математиком и астрономом. Эта дружба длилась многие годы.
Эратосфен прославился вычислением длины меридиана земного ша¬ра. Одно из его писем Архимеда к Эратосфену сохранилось до наших дней. Из сохранившихся писем Архимеда, в которых он обсуждает важные математические проблемы, видно, что он предвосхитил идеи дифференциального и интегрального исчислений.
После учёбы в Александрии Архимед вновь вернулся в Сиракузы и унаследовал должность своего отца.
Архимед провёл жизнь в Сиракузах, где пользовался необыкновенной любовью и уважением сограждан. Сиракузцы Архимеда называли „Старик".

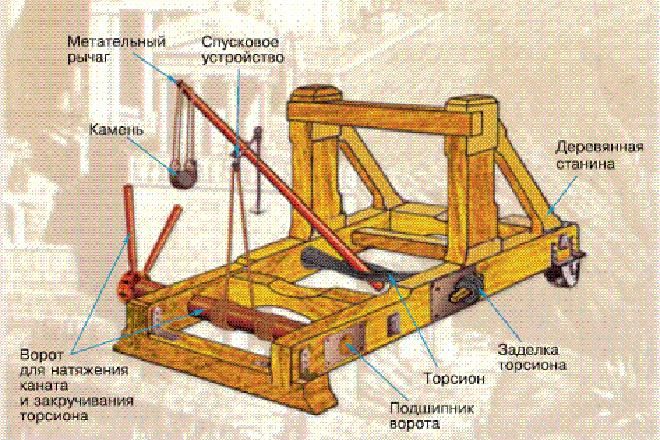
Инженерный гений Архимеда с особой силой проявился во время осады Сиракуз римлянами в 212 году до н. э. в ходе Второй Пунической войны А ведь в это время ему было уже 75 лет! Построенные Архимедом мощные метательные машины забрасывали римские войска тяжёлыми камнями. Думая, что они будут в безопасности у самых стен города, римляне кинулись туда, но в это время лёгкие метательные машины близкого действия забросали их градом ядер.
Мощные краны захватывали железными крюками корабли, приподнимали их кверху, а затем бросали вниз, так что корабли переворачивались и тонули. В последние годы были проведены несколько экспериментов с целью проверить правдивость описания этого «сверхоружия древности». Построенная конструкция показала свою полную работоспособность.
Архимед создал метательные машины, способные бросать с большой скоростью камни массой около 250 кг и механизмы, бросающие с берега на суда тяжёлые брёвна. Римляне вынуждены были отказаться от мысли взять город штурмом и перешли к осаде. Знаменитый историк древности Полибий писал: «Такова чудесная сила одного человека, одного дарования, умело направленного на какое-либо дело… римляне могли бы быстро овладеть городом, если бы кто-либо изъял из среды сиракузян одного старца».

Во многом благодаря Архимеду, осада Сиракуз затянулась на 8 месяцев. Римский полководец Марцелл, командующий осадой Сиракуз, сказал: «Придется нам прекратить войну против геометра». Город пал только благодаря предательству (и пассивности карфагенян) осенью 212 года до н. э. Это произошло во время праздника Артемиды, когда охранники были пьяны. Один из охранников открыл врагу потайной ход в стене.

Из описания Полибием осады видно, что Архимед руководил обороной города, хотя власть в Сиракузах в то время принадлежала Гиппократу и Эпикиду.
Плутарх приводит три существовавших версии о гибели сиракузского учёного. Учёный работал над какой-то геометрической проблемой и так был погружен в неё, что не заметил, как римляне захватили город. Появившийся перед ним римский солдат приказал идти с ним к военачальнику Марцеллу и наступил на чертёж, сделанный Архимедом на пыльной земле. Архимед воскликнул: "Не тронь моих чертежей” (Noli turbare circulos meos!). Солдат выхватил свой меч и убил безоружного семидесятипятилетнего геометра.
По другой, описанной у Плутарха, версии Архимед перед гибелью просил солдата немного обождать, чтобы задача, которой он был на тот момент занят, получила решение.
И по третьей плутарховой версии Архимед сам отправился к Марцеллу со своими математическими приборами. Легионеры решили, что старик несёт что-то ценное и убили его с целью грабежа. Полибий и Плутарх подчёркивают, что главнокомандующий римской армией Марцелл был опечален случившимся, так как якобы приказал не убивать Архимеда во время штурма.
Архимед жил в эпоху, когда развитие техники поставило перед математикой множество задач. Гидротехника, военная техника, морской транспорт, астрономия, геодезия, картография, механика, оптика потре¬бовали от учёных решения практических задач. Поэтому работы Архимеда не могли ограничиваться теоретическими рассуждениями, но должны были отвечать потребностям жизни.
Архимед писал свои сочинения малодоступным языком, пропуская лёгкие, по его мнению, звенья. Поэтому его труды не имели широкого распространения.

Архимед нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений вида , корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провёл и полное исследование этих уравнений, то есть нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать.
В сочинении «Квадратура параболы» Архимед доказал, что площадь сегмента параболы, отсекаемого от неё прямой, составляет 4/3 от площади вписанного в этот сегмент треугольника. Для доказательства Архимед подсчитал сумму бесконечного ряда: .
Каждое слагаемое ряда — это общая площадь треугольников, вписанных в неохваченную предыдущими членами ряда часть сегмента параболы.

Главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа. Греки до Архимеда сумели определить площади многоугольников и круга, объём призмы и цилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей или объёмов; для этого он усовершенствовал и виртуозно применял метод исчерпывания Евдокса Книдского. В своей работе «Послание к Эратосфену о методе» (иногда называемой «Метод механических теорем») он использовал бесконечно малые для вычисления объёмов. Идеи Архимеда легли впоследствии в основу интегрального исчисления.
Математикой Архимед начал заниматься под влиянием александрийского математика Конона. Он был в переписке с учеником Конона Досифеем, который заведовал Александрийской библиотекой.

Ряд работ Архимеда, посвященных нахождению площадей и объёмов, прославили его как предшественника создателей дифференциального и интегрального исчислений Ньютона и Лейбница, до которых было ещё долгих 2000 лет.
Сам Архимед своим крупнейшим достижением считал доказательство теоремы о том, что объёмы шара и описанного вокруг него цилиндра относятся как 2:3. Поэтому он просил поместить на своей гробнице рисунок шара, вписанного в цилиндр.
Архимед сумел установить, что сфера и конусы с общей вершиной, вписанные в цилиндр, соотносятся следующим образом: два конуса : сфера : цилиндр как 1:2:3.
Установив, что отношение длины окружности к её диаметру меньше и больше , Архимед тем самым нашёл приближенное значение числа π. Наиболее известно приближение числа π (22/7), которое называется Архимедовым числом.
Архимед нашёл и формулу для вычисления площади треугольника по трём сторонам:
где полупериметр треугольника.
Это соотношение носит название формулы Герона, в честь Герона Александрийского, греческого механика, жившего в I веке новой эры, который в своем труде «Механика» привел отрывки из работ Архимеда. Герон сделал эту формулу популярной. Можно сказать, что он второй раз её открыл.
Утверждение: «Все 3 высоты треугольника пересекаются в одной точке», называемой теперь ортоцентром, часть историков приписывает Архимеду и называют его теоремой Архимеда. Ортоцентр впервые в греческой математике использован в «Книге лемм» Архимеда, хотя явного доказательства существования ортоцентра Архимед не привёл. Тем не менее до середины девятнадцатого века, ортоцентр нередко называли архимедовой точкой.

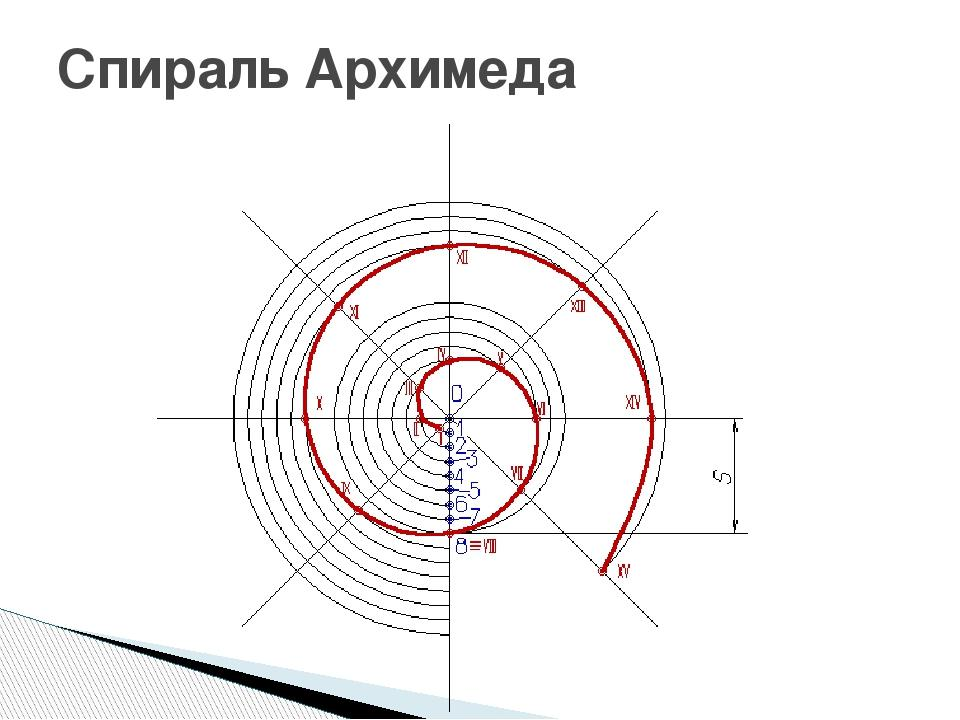
Помимо перечисленного, Архимед вычислил площадь поверхности для сегмента шара и витка открытой им «спирали Архимеда», определил объёмы сегментов шара, эллипсоида, параболоида и двуполостного гиперболоида вращения.
В течение многих веков основой механики была изложенная в труде Архимеда «О равновесии плоских фигур» теория рычага. В основе этой теории лежат следующие постулаты:
Равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивают тяжести на большей длине;
Если при равновесии тяжестей на каких-нибудь длинах к одной из тяжестей будет что-нибудь прибавлено, то они не будут уравновешиваться, но перевесит та тяжесть, к которой было прибавлено;
Точно так же если от одной из тяжестей будет отнято что-нибудь, то они не будут уравновешиваться, но перевесит та тяжесть, от которой не было отнято.
На основании этих постулатов Архимед сформулировал закон рычага следующим образом: «Соизмеримые величины уравновешиваются на длинах, которые будут обратно пропорциональны тяжестям. Если величины будут несоизмеримы, то они точно так же уравновесятся на длинах, которые обратно пропорциональны этим величинам».

"Дайте мне точку опоры, и я подниму Землю!" - такое восклицание легенда приписывает Архимеду. Но если бы великий механик древности знал, как огромна масса земного шара, он, вероятно, воздержался бы от своего горделивого восклицания. Вообразим на мгновение, что Архимеду дана та "другая Земля", та точка опоры, которую он искал; вообразим далее, что он изготовил рычаг нужной длины. Знаете ли, сколько времени понадобилось бы ему, чтобы груз, равный по массе земному шару, поднять хотя бы на 1 см? Не менее тридцати тысяч биллионов лет! В самом деле. Масса Земли известна; тело с такой массой весило бы на Земле круглым счетом Если человек может непосредственно поднять груз весом 60 кгс, то, чтобы "поднять Землю", ему понадобится приложить свои руки к длинному плечу рычага, которое больше короткого в 1023 раз!
Простой расчёт убедит вас, что, пока конец короткого плеча поднимается на 1 см, другой конец опишет во Вселенной огромную дугу в 1018 км. Такой невообразимо длинный путь должна была бы пройти рука Архимеда, налегающая на рычаг, чтобы "поднять Землю" только на 1 см! Сколько же времени понадобится для этого? Если считать, что Архимед способен был поднять груз весом 60 кгс на высоту 1 м за 1 секунду, то и тогда для "поднятия Земли" на 1 см потребуется 1021 секунд, или тридцать тысяч биллионов лет! За всю свою долгую жизнь Архимед, напирая на рычаг, не "поднял бы Земли" даже на толщину тончайшего волоса...

Никакие ухищрения гениального изобретателя не помогли бы ему заметно сократить этот срок. "Золотое правило механики" гласит, что на всякой машине выигрыш в силе неизбежно сопровождается соответствующей потерей в длине перемещения, т. е. во времени. Если бы даже Архимед довёл быстроту своей руки до величайшей скорости, какая возможна в природе, до 300000 км/с (скорость света), то и при таком фантастическом допущении он "поднял бы Землю" на 1 см лишь после десяти миллионов лет работы.
В трудах „Книга опор” и „О рычагах” Архимед разработал теорию центров тяжести тел. Там дано определение центра тяжести тела как «некоторая расположенная внутри его [тела] точка — такая, что если за неё мысленно подвесить тело, то оно остаётся в покое и сохраняет первоначальное положение». Также им были описаны принципы расчёта центра тяжести треугольника, параллелограмма, трапеции, сегмента параболы, криволинейной трапеции, боковые стороны которой являются дугами парабол.
Изложенные Архимедом принципы работы рычагов и понятие центра тяжести практически в неизменном виде используются и на сегодняшний день.

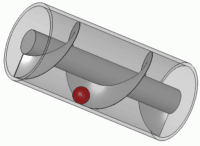
Архимеду принадлежит изобретение машины для орошения полей (архимедов винт). Изобретение бесконечного винта привело его к другому важному изобретению, пусть даже оно и стало обычным, — к изобретению болта, сконструированного из винта и гайки.
Древнегреческий писатель Афиней (II—III века н. э.) описал, как царь Гиерон II поручил учёному спроектировать громадный по античным меркам корабль «Сиракузию». Судно предполагали использовать во время увеселительных путешествий, а также для перевозки грузов и солдат. По современным оценкам роскошный корабль, отделанный драгоценными камнями и слоновой костью, имел длину около 100 метров и мог перевозить до 5 тысяч человек.
Согласно Афинею на корабле были сад, гимнасий и даже посвящённый Афродите храм. Предполагалось, что такое судно будет давать течь. Разработанный Архимедом винт позволял выкачивать воду всего лишь одному человеку.
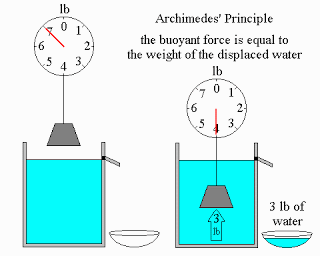
Это устройство представляло собой вращающийся внутри цилиндра винт с косым направлением витков резьбы. Строение архимедова винта дошло до нас из трудов римского архитектора и механика I века до н. э. Витрувия. Несмотря на кажущуюся простоту, данное изобретение позволило решить поставленную перед учёным проблему. Его впоследствии стали применять в самых различных отраслях народного хозяйства и промышленности, в том числе и для перекачки жидкостей и сыпучих твёрдых веществ, таких как уголь и зерно. Первенство Архимеда в его открытии оспаривается. Возможно, архимедов винт представляет собой несколько модифицированную систему водяного насоса, который использовали при орошении построенных задолго до корабля «Сиракузия» висячих садов Семирамиды в Вавилоне.
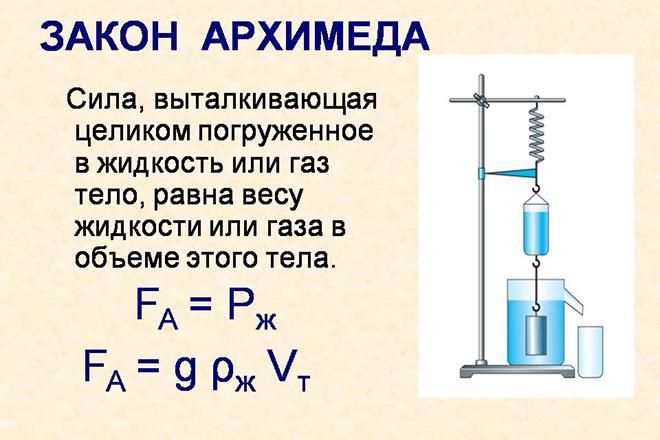
Самый известный рассказ об Архимеде – это рассказ Витрувия о происхождении возгласа "Эврика!", хотя историки и сомневаются в достоверности этого события. Архимед вывел известный закон, носящий его имя: всякое тело, погружённое в воду, теряет в своем весе столько, сколько весит вытесненная им вода. Говорят, что Гиерон попросил однажды Архимеда проверить, не добавил ли мастер серебра к слитку, из которого делал царю золотую корону. Архимед долго думал над этой задачей. Решение пришло неожиданно, когда он сидел в ванне. Ошеломлённый открытием, Архимед с криком „Эврика!” (нашёл) выскочил из ванны и нагишом выбежал на улицу. Закон Архимеда позволяет определять удельный вес тел. Поэтому достаточно было сравнить удельный вес короны с удельным весом золота, чтобы решить задачу Гиерона.
Архимеду принадлежат слова: „Дайте мне точку опоры, и я сдвину Землю”. Рабочие не могли спустить на воду трёхмачтовый корабль, так тяжел он был. Архимед легко справился с этой задачей, применив систему блоков, установленных на суше в отдалении от корабля.
Восхищенный этим изобретением Гиерон заказал у Архимеда ряд механизмов для защиты города во время его осады. Архимед изобрёл разного вида катапульты, которые были с успехом применены во время пунических войн. При осаде Сиракуз войсками Марцелла на римлян сыпались камни и брёвна, метаемые машинами Архимеда. Архимед впервые устроил бойницы в стенах крепостей. До этого строили только сплошные стены (огнестрельное оружие появилось в средние века). По словам Прокла, с помощью системы зеркал и линз поджигались корабли.
Снабжённые крючьями системы блоков (полиспасты) опрокидывали римские корабли. Архимед два года успешно руководил обороной Сиракуз. Лишь напав неожиданно на город с тылу, Марцелл одержал победу. Чем это закончилось для Архимеда, мы уже знаем.
У эллинов и средневековых арабов Архимед вызывал такие же чувства, какие в 17-ом веке у учёных вызывал И. Ньютон, а в 19-ом веке — К. Гаусс.
Хотя Архимед, этот аристократ духом и телом, был одним из величайших гениев механики всех времён, он искренне презирал свои практические изобретения.
Архимед, подобно позже Ньютону и Гамильтону, забывал о еде, когда погружался в математические исследования. В небрежности отношения к своей одежде он даже превосходил Ньютона.
Велик вклад Архимеда в астрономию и прикладную механику. До сегодняшнего дня дошли сведения о трёх астрономических работах Архимеда . В сочинении «Псаммит» он задался вопросом о размере Вселенной. Ипполит Римский (170—230-е годы н. э.) в приписываемом ему трактате «Обличение всех ересей» приводит расстояния между планетами, взятыми из какой-то из утерянных ныне работ Архимеда. Также сохранились четыре упоминания о своеобразном планетарии или «небесном глобусе», сконструированным Архимедом.
В «Псаммите» он экспериментальным путём нашёл угловой диаметр Солнца — от 27’ до 32’55". Истинное значение показателя составляет 31’28"—32’37". То есть, как подчёркивают современные авторы, Архимеду удалось впервые определить данную величину.
Архимед построил планетарий или «небесную сферу», при движении которой можно было наблюдать движение пяти планет, восход Солнца и Луны, фазы и затмения Луны, исчезновение обоих тел за линией горизонта. Занимался проблемой определения расстояний до планет; предположительно в основе его вычислений лежала система мира с центром в Земле, но планетами Меркурием, Венерой и Марсом, обращающимися вокруг Солнца и вместе с ним — вокруг Земли. В своём сочинении «Псаммит» донёс информацию о гелиоцентрической системе мира Аристарха Самосского.
Сведения о некоем «небесном глобусе», который наглядно изображал систему мира с Землёй в центре, вокруг которой вращаются Солнце, Луна и
планеты, содержатся в нескольких античных источниках. Цицерон, в пересказе, передаёт слова Гая Сульпиция Галла, который якобы видел в доме Марцелла устройство, сконструированное Архимедом, и привезённое завоевателем Сиракуз в качестве трофея. Одновременно он говорит о более известной «другой сфере Архимеда», которую Марцелл передал в храм Доблести. Это устройство упоминали Овидий, Лактанций и Клавдий Клавдиан
Клавдиан описывает работу «небесного глобуса» через 6 веков после смерти Архимеда. Все из перечисленных авторов изумлены и восхищены данным устройством. «Если в мире это [движение планет] не может совершиться без бога, то и в сфере своей Архимед не мог бы воспроизвести это без божественного вдохновения», — резюмирует описание архимедова шара Цицерон.
Архимед владел методом приближённого вычисления квадратных корней, в арифметике далеко превзошёл неудобный греческий метод представления чисел, применил законы рычага к вычислению площадей плоских фигур и объёмов тел различной формы, к отысканию их центров тяжести, сформулировал условия плавания тел.
Путём логических рассуждений, а также на основе их подтверждения в экспериментах, Архимед пришёл к выводам, что более лёгкое, относительно воды, тело погружается до тех пор, пока вес жидкости в объёме погрузившейся части не станет равным весу всего тела. Исходя из этого он пишет утверждения, содержащие формулировки названного в его честь закона гидростатики: «Тела более лёгкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх с силой, равной тому весу, на который жидкость, имеющая равный объём с телом, будет тяжелее этого тела» и «Тела более тяжёлые, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объёме, равном объёму погружённого тела».
Решая задачу о построении касательной к спирали в произвольной её точке, Архимед подошёл к открытию дифференциального исчисления. Спираль Архимеда - это кривая, образованная точкой, движущейся равномерно вдоль прямой линии, которая вращается с постоянной угловой скоростью вокруг фиксированной точки на этой прямой.
В работе „О спиралях” он писал: „Если в плоскости заставить вращаться равномерным движением прямую вокруг одной неподвижной из её точек до возвращения её в первоначальное положение и если вдоль перемещающейся прямой заставить одновременно двигаться от неподвижной точки, также равномерно, некоторую точку, то последняя опишет спираль”.
Архимед внёс движение в определение спирали. До него в работах даже таких выдающихся геометров, как Евклид, движение совершенно игнорировалось. Введя в геометрию движение, Архимед способствовал этим более быстрому развитию геометрии. Плутарх писал о математических открытиях Архимеда: „Во всей геометрии нет теорем более трудных и более глубоких, нежели теоремы Архимеда".
(Окончание следует)
