СОЗДАТЕЛЬ МАТЕМАТИЧЕСКОЙ НАУКИ О МЕХАНИЗМАХ

Жизнь Пафнутия Львовича Чебышева небогата внешними событиями. Русский математик и механик, академик Петербургской АН Пафнутий Львович Чебышев (Чебышёв) родился 4 (16) (в некоторых источниках приводится дата 14 (26)) мая 1821 г. в селе Окатово Боровского уезда Калужской губернии в семье богатого землевладельца Льва Павловича Чебышёва. Почему новорожденного назвали редко встречающимся именем Пафнутий, трудно сказать. Вероятно, потому, что недалеко от Окатова находился Пафнутьев монастырь, чтимый родом Чебышёвых. Отец будущего математика Лев Павлович в двадцать лет был лихим кавалерийским корнетом, участвовал в сражениях против французов. Потом вышел в отставку, поселился в своём имении и занялся хозяйством. Окружающие считали его хорошим человеком. А вот Аграфену Ивановну, мать Пафнутия, не лю6или за жестокость и надменность, и даже близкие родственники, особенно кто победнее, на её расположение никогда не рассчитывали.

            Детство Пафнутия Львовича прошло в старом огромном доме. Комнат в нём, казалось, было бесчисленное множество, а длинные полутёмные коридоры по вечерам внушали мальчишкам благоговейный страх, который утром казался им смешным и нелепым. На месте, где он стоял почти полтора века, Пафнутий Львович с младшими братьями установят потом, громадную гранитную глыбу, на которой высекут слова: "Здесь у Льва Павловича и Аграфены Ивановны Чебышёвых родилось пятеро сыновей и четыре дочери". Камень и сейчас там стоит.

      Начальное образование Пафнутий получил в семье. Грамоте его обучила мать Аграфена Ивановна, арифметике и французскому языку — двоюродная сестра Авдотья Квинтильановна Сухарёва, женщина образованная, сыгравшая большую роль в его жизни. Её портрет висел в доме Чебышёва до самой его кончины. 

        В детстве его постоянным другом был перочинный ножик, которым он орудовал с искусством виртуоза. Он часами просиживал, строгая и мастеря разного рода деревянные механизмы. Так, с большим мастерством он изготовил водяную и ветряную мельницы со всеми их передаточными механизмами. Страсть к изобретательству и конструированию у него сохранилась на всю жизнь. Будучи уже прославленным математиком, он много времени и средств тратил на изготовление механизмов собственного изобретения. Прекрасное знание математики помогло ему конструировать весьма сложные механизмы, и, наоборот, изготовленные им модели способствовали нахождению новых проблем математики, над решением которых трудился он сам и его ученики.

         Кроме того, с детства Пафнутий Львович занимался музыкой.

С детства Чебышёв прихрамывал, часто пользовался тростью. Этот физический недостаток помешал ему стать офицером, о чём он некоторое время мечтал.

В десятилетнем возрасте Чебышёв со своим дядей совершил длительную поездку на Кавказ.

В 1832 г. семья Чебышёвых переехала в Москву для подготовки Пафнутия и его брата к поступлению в университет. В Москве с Пафнутием математикой и физикой занимался П. Н. Погорельский, один из лучших учителей Москвы.

           В 1837 г. он поступил в Московский университет. Будучи студентом, он в точности исполнял все требования правил поведения: посещать лекции, носить треугольную шляпу, быть всегда в застёгнутом вицмундире. На протяжении четырёх лет учёбы он имел "отличные успехи" и "был отличного поведения". Ещё студентом он получил серебряную медаль за работу "Вычисление корней уравнений n-й степени''. Одним из тех, кто повлиял на него в этот период в наибольшей степени, был Николай Брашман, который познакомил его с работами французского инженера Жана-Виктора Понселе.

В 1840 г. материальное положение семьи Чебышёвых ухудшилось: пока Чебышёв учился в университете, в России грянул голод, и родители разорились. Пафнутий был вынужден жить на собственный заработок. Это наложило отпечаток на его характер, сделав его расчетливым и бережливым. Впоследствии, не испытывая недостатка в средствах, он не соблюдал экономии в их расходовании только при изготовлении моделей различных приборов и механизмов.

В 1841 г. он окончил университет и в 1846 г. защитил магистерскую диссертацию "Опыт элементарного анализа теории вероятностей''.

       Младшие братья Чебышёва, Николай и Владимир, решили стать офицерами, поступив в Петербургское артиллерийское училище. Пафнутий решает быть ближе к младшим братьям. В 1847 г. он тоже переехал в Петербург и начал читать лекции по аналитической геометрии, алгебре и теории чисел в Петербургском университете, где он проработал 35 лет.

       Работая в Петербургском университете, Чебышёв близко сошёлся с профессором прикладной математики О. И. Сомовым, который тоже был учеником Н. Д. Брашмана, и эти отношения переросли в глубокую дружбу. В семейном плане Чебышёв был одинок, и это обстоятельство также способствовало его сближению с большой семьёй Сомова.

            С 1850 г. Чебышёв - профессор. Его докторская диссертация "Теория сравнений" была отмечена Петербургской АН Демидовской премией, вошла во все мировые учебники по теории чисел и сразу стала классикой. Долгое время Чебышёв работал в Учёном комитете Министерства народного просвещения. С 1882 г. он перестаёт читать лекции в университете и сосредотачивается на работе в Академии наук.

     В 1851 году появился знаменитый его мемуар «Об определении числа простых чисел, не превосходящих данной величины». Этот мемуар принёс 30-летнему Чебышёву общеевропейскую известность. В следующем, 1852 году Чебышёв опубликовал новую статью «О простых числах». В ней он провёл глубокий анализ сходимости рядов, зависящих от простых чисел, нашёл критерий их сходимости.

     Начало рабор Чебышёва по теории чисел положено в прибавлениях к докторской диссертации Чебышёва: «Теория сравнений», напечатанной в 1849 году.

          Трудно указать другое понятие, столь же тесно связанное с возникновением и развитием человеческой культуры, как понятие числа. Недаром древние греки приписывали легендарному Прометею, среди прочих его бессмертных деяний, изобретение числа.

       Особенное значение уже в древней Греции получило исследование простых чисел, т. е. чисел, делящихся без остатка лишь на себя и на единицу. Все остальные числа являются, следовательно, произведениями простых чисел, и, значит, простые числа являются теми элементами, из которых образовано каждое целое число. Древнегреческой математике, пожалуй, был известен только один общий результат о простых числах, известный теперь под названием теоремы Евклида. Согласно этой теореме, в ряду целых чисел имеется бесконечное множество простых. На вопросы же о том, как расположены эти числа, сколь правильно и как часто, греческая наука не имела ответа.

       Около двух тысяч лет, прошедших со времени Евклида, не принесли сдвигов в эти проблемы, хотя ими занимались многие математики и среди них такие корифеи математической мысли, как Л.Эйлер и К.Ф.Гаусс. Эмпирические подсчёты, произведённые Лежандром и Гауссом, привели их к выводу, что в пределах известных им таблиц простых чисел число простых чисел среди всех первых n чисел приблизительно в ln n раз меньше, чем число l.

      Это утверждение оставалось чисто эмпирическим фактом, установленным лишь для чисел в пределах миллиона. Переносить его на большие значения n не было никаких оснований, путей же для строгого доказательства не было видно.

        Число простых чисел, не превышающих заданного натурального n, обозначается символом π(n). Конечно, некоторые значения этой функции π(n) можно точно установить по таблице простых чисел. Так, например, на отрезке [1; 10] π(10)=4 (2; 3; 5; 7); на отрезке [1; 100] π(100)=25; на отрезке [1; 106] π(106) =78498 простых чисел и т.д.

          После Евклида (III век до н.э.), доказавшего изящным строгим рассуждением, что в последовательности простых чисел нет наибольшего, стало ясным, что π(n) неограниченно возрастает с возрастанием n; но по какому же закону?

      Век следовал за веком, и только Чебышёву удалось первым «прорубить окно» в таинственную и казавшуюся неприступной область теории распределения простых чисел. С большим остроумием и глубиной анализа он доказал, что при достаточно больших значениях n истинное значение π(n) находится вблизи числа

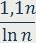
точнее,

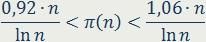
– неравенство Чебышёва.

       Более того, средствами, продолжающими по существу идеи Чебышева, опирающимися на его неравенство, оказалось возможным доказать предельное соотношение

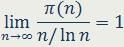
почти через 100 лет после того, как это утверждение было высказано Чебышёвым в 1849 году, но полностью им не обосновано.

      В 1850 году появилась знаменитая работа Чебышёва, где даны асимптотические оценки для суммы ряда

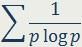
по всем простым числам p.

        Результаты, полученные Чебышёвым в теории чисел, восторгали его современников. Английский математик Джеймс Джозеф Сильвестр писал: «Чебышёв – князь и победитель простых чисел, способный справиться с их непокорным характером и совладать с потоком их переменчивых движений и двигаться вперёд в алгебраических пределах.»

      В 1852 году Чебышёв совершил научную командировку в Великобританию, Францию и Бельгию, в ходе которой он ознакомился с практикой зарубежного машиностроения, с музейными коллекциями машин и механизмов, с работой заводов и фабрик, а также встречался с крупнейшими математиками и механиками: О. Коши, Ж. Лиувиллем, Ж.-А. Серре, Л. Фуко, Ш. Эрмитом, Дж. Сильвестром, А. Кэли, Т. Грегори. После этого он некоторое время преподавал практическую механику в Петербургском университете и Александровском лицее, что находится в Царском Селе.

        В 1853 году академики П. Н. Фусс, В. Я. Струве, Б. С. Якоби, В. Я. Буняковский представили Чебышёва к избранию в адъюнкты Петербургской академии наук, особо отметив важность его работ в области практической механики. В том же году он был избран в адъюнкты, а в 1856 году стал экстраординарным академиком.

        В 1858 году в связи с его работами по теории шарнирных параллелограммов и теории приближения функций академики В. Я. Буняковский, М. В. Остроградский, Э. Х. Ленц, Б. С. Якоби, А. Я. Купфер, О. В. Струве подписали представление к избранию Чебышёва ординарным академиком, что и произошло в следующем году. Почётный член Московского университета (1858). С 22 февраля 1860 года — ординарный профессор; с 10 июля 1863 года — член Учёного комитета Министерства народного просвещения; с 30 августа 1863 года — действительный статский советник.

В 1863 году особая «Комиссия Чебышёва» принимала деятельное участие от Совета Санкт-Петербургского университета в разработке Университетского устава. Университетский устав, подписанный Александром II 18 июня 1863 года, предоставлял автономию университету как корпорации профессоров. Этот устав просуществовал до эпохи контрреформ правительства Александра III и рассматривался историками как наиболее либеральный и удачный университетский регламент в России XIX — начала XX веков.

П.Л.Чебышёв - основатель петербургской математической школы. Его отличает разнообразие областей исследования, умение получать элементарными средствами большие научные результаты и неизменный интерес к практическим вопросам. Он написал более 70 научных работ.

В каждом из рассматриваемых им разделов математики - теория приближения функций многочленами, интегральное исчисление, теория чисел, теория вероятностей, теория механизмов и др. - он сумел создать ряд общих методов и выдвинул идеи, наметившие направления их развития. Для него характерно стремление увязать проблемы математики с вопросами естествознания.

Современники называли Чебышева «кочующим математиком».

Имелось в виду то, что он был одним из тех учёных, которые видят своё призвание, прежде всего, в том, чтобы, переходя из одной области науки в другую, в каждой оставить ряд блестящих идей или методов, долго ещё воздействующих на воображение исследователей. Оригинальные идеи Чебышёва моментально подхватывались его многочисленными учениками, становясь достоянием всего научного мира.

   Чебышёв стал первым русским математиком мирового уровня и в теории вероятностей.  К теории вероятностей тянутся нити буквально от всех областей знания. Эта наука занимается изучением случайных явлений, течение которых нельзя предсказать заранее и осуществление которых при совершенно одинаковых условиях может протекать совершенно различно, в зависимости от случая. Два основных закона этой науки - закон больших чисел и центральная предельная теорема - ведут своё начало от П. Л. Чебышёва.

Чебышёв возбудил интерес к теории вероятностей и создал школу своих последователей, он впервые придал ей лицо настоящей математической науки. Дело в том, что в эпоху, когда П. Л. Чебышёв начинал своё творчество, теория вероятностей как математическая дисциплина находилась в младенческом состоянии, не имея собственных достаточно общих задач и методов исследования.

       С 1860 года он сменил В. Я. Буняковского на кафедре теории вероятностей Петербургского университета и начал свой цикл лекций. Он опубликовал по данной теме всего четыре работы, но фундаментального характера.

      В 1867 году во II томе «Московского Математического Сборника» появился мемуар Чебышёва «О средних величинах», в котором дана теорема, лежащая в основе различных вопросов теории вероятностей и заключающая в себе знаменитую теорему Якова Бернулли как частный случай. Доказанное там «неравенство Чебышёва», позднее было усилено Марковым.

       П.Л.Чебышёв доказал закон больших чисел (частота события будет сколько угодно близкой к её вероятности, если число испытаний неограниченно растёт) с поразительной простотой и элементарностью.

      На базе его работ выросла русская школа теории вероятностей. Получившее в Литве большое развитие теоретико-вероятностное направление в теории чисел, также связано с этой школой.

     Чебышёв много занимался теорией квадратичных форм и связанными с ней проблемами делимости натуральных чисел и их разложения на простые множители. В своей статье 1866 года «Об одном арифметическом вопросе» он, используя аппарат непрерывных дробей, исследовал диофантовы приближения целых чисел. В аналитической теории чисел он одним из первых использовал гамма-функцию.

П.Л.Чебышёв, впервые после Евклида, существенно продвинул изучение вопроса о распределении простых чисел. Он доказал так называемый постулат Бертрана, который утверждает, что между числами n и 2n-2 при n больше 3 всегда есть хотя бы одно простое число, а также важную теорему о распределении простых чисел в натуральном ряде. Он установил асимптотический закон распределения простых чисел. Чебышёв является создателем новых направлений и новых методов в теории чисел. При этом поражает способность Чебышёва простыми, элементарными средствами получать великолепные научные результаты.

       Многие работы Чебышёва посвящены математическому анализу — в частности, работы по построению общей теории ортогональных многочленов. Одним из любимых приёмов Чебышёва, которым он особенно часто пользовался, было приложение свойств алгебраических непрерывных дробей к различным вопросам анализа.

          П.Л.Чебышёв - основоположник конструктивной теории функций, основным составным элементом которой является теория наилучших приближе¬ний функций многочленами. П. Л. Чебышёв поставил и решил задачу о нахождении многочленов, наименее уклоняющихся от нуля. Профессор Феликс Клейн в своих лекциях, прочитанных в Гёттингенском университете в 1901 году, называл этот результат «удивительным». Его содержание вошло во многие классические монографии. В связи с этими же вопросами находится и работа Чебышёва «О черчении географических карт».

      Введённые П. Л. Чебышёвым многочлены, наименее уклоняющиеся от нуля, получили применение, в частности, в вычислительной линейной алгебре. Именно, начиная с 1950-х годов при решении систем линейных уравнений получил распространение чебышёвский итерационный метод. Это — видоизменение метода простых итераций. Рассматривавшиеся им многочлены теперь называют полиномами Чебышёва.

     В 1887 году появилась статья Чебышёва «О двух теоремах относительно вероятностей». В этой работе он установил, что при некоторых (достаточно общих) условиях выполняется центральная предельная теорема: сумма большого числа независимых случайных величин с нулевыми математическими ожиданиями (например, погрешностей измерения) распределена приближённо по нормальному закону, и тем точнее, чем больше слагаемых в сумме. Этот результат по своей общности далеко перекрывает теорему Муавра — Лапласа и все её аналоги. В ходе поисков доказательства теоремы Чебышёв разработал — для случая сходимости к нормальному распределению — метод, известный сейчас как метод моментов, то есть метод определения распределения вероятностей по его моментам.

      Доказывая свой вариант центральной предельной теоремы, Чебышёв допустил логический пробел: оказалось, что — в дополнение к указанным Чебышёвым условиям применимости теоремы — следует ещё потребовать, чтобы среднее арифметическое дисперсий при стремлении к бесконечности имело предел. Данный недостаток был вскоре исправлен А. А. Марковым.

Обе упомянутые теоремы Чебышёва занимают центральное место в теории вероятностей. Особенно важно то обстоятельство, что Чебышёв не только указал предельное распределение, но в обоих случаях детально проанализировал границы возможных отклонений от этого предела.

         В теории вероятностей Чебышеву удалось необычайно простыми средствами получить ряд весьма важных результатов. Многие результаты и выводы были только намечены, не доведены до конца, но все работы Чебышёва в этой области явились той базой, на которой развилась русская школа теории вероятностей. Строгие доказательства многих теорем, намеченные Чебышевым, и дальнейшее их развитие было проведено его учениками, академиками А. М. Ляпуновым и А. А. Марковым.

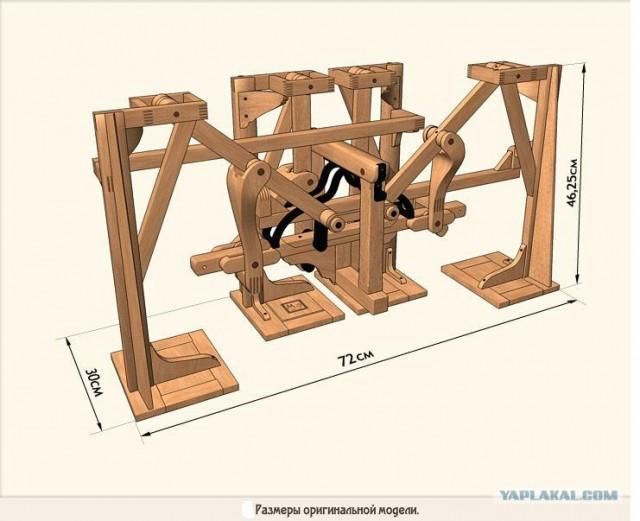
            П.Л.Чебышёв постоянно интересовался теорией машин и механизмов, много работ он посвятил синтезу шарнирных механизмов. В работе по конструированию он уделял большое внимание так называемым параллелограммам, т. е. механизмам для преобразования кругового движения в прямолинейное и наоборот. Он создал более 40 новых механизмов и усовершенствовал более 80. Интересны созданные им автоматический арифмометр, стопоходящая машина. Созданные им механизмы демонстрировались на выставках в Париже (1878г.) и в Чикаго (1893г.).

        Несмотря на летнюю жару, выставка в Чикаго проходила при большом скоплении народа. Особенно людно было в павильоне, где демонстрировались удивительные механизмы, привезённые из далекой России. Вот «стопоходящая» машина, довольно точно воспроизводящая шаги четвероногого животного. А вот самоходное кресло. Можно сесть в него и передвигаться в любом направлении. Привлекла внимание зрителей лодка с гребным механизмом. Один учёный, увидев эту лодку, воскликнул: «Я в восторге от вашей лодки с ногами, которая пойдет по воде, как лошадь!»

         Здесь на выставке можно было видеть усовершенствованный центробежный регулятор и многое другое. Всеобщее удивление посетителей выставки вызвала, как и следовало ожидать, счётная машина, или арифмометр, выполняющий быстро и совершенно точно четыре арифметических действия.

        Изобретателем этих оригинальных механизмов был Пафнутий Львович Чебышёв, по праву считавшийся «отцом современной теории механизмов». В истории развития науки о машинах нельзя указать ни одного учёного, творчеству которого принадлежало бы столь значительное количество оригинальных механизмов. Под влиянием дискуссий с Чебышёвым, вопросами кинематики механизмов заинтересовались британские ученые Джеймс Сильвестр и Артур Кэли.

П. Л. Чебышёв, как уже упоминалось, был хром на одну ногу. Может быть, благодаря этому он не выносил шумного общества друзей и любил уединенный образ жизни, предаваясь своим мечтам и размышлениям.

Большое практическое применение имеет разработанная им методика построения выкроек. Его работа "О кройке одежды" имеет тесную связь с теорией построения механизмов. Подобно тому, как механизмы создаются из прутьев, длина которых не меняется, а изменяются углы наклона между ними, так и при выделке платьев длины нитей остаются неизменными, а изменяются углы между нитками утка и основы.

Связав вопросы кройки с теорией поверхностей, Чебышев установил основные принципы, по которым должны строиться разрезы материи для создания оболочки, в которую с наименьшим отклонением должно быть помещено одеваемое тело.

В упоминавшейся статье о дифференциальной геометрии, под названием «О кройке одежды» он представил новый класс координатных сеток – «сетей Чебышёва».

    Чебышёв жил в тот век, который английский физик лорд Рэлей охарактеризовал эпохой, в которой всё вращается. Появилась необходимость преобразовывать круговые движения в прямолинейные, что и воплотилось в механизмах Чебышёва. А создание механизмов привело к необходимости развития теории приближенных выражений функций. Эта теория и содержала наиболее оригинальные идеи Чебышёва.

В 1860г. Чебышёв был избран членом-корреспондентом Парижской Академии наук, в связи с чем получил письмо от французского математика, признанного лидера математиков Франции во второй половине XIX века, Шарля Эрмита: "Я счастлив известить Вас об избрании. Эта дань уважения вполне заслуженная и должная, которая была воздана Вашим прекрасным открытиям в арифметике и Вашим важным работам по теории интегрирования".

Имея немалый доход как профессор и академик и гонорары от публикаций, Чебышёв большую часть зарабатываемых денег употреблял на покупку земель. Этими операциями занимался его управляющий, затем выгодно перепродававший скупленные земли.

Работы П.Л.Чебышёва ещё при жизни нашли широкое признание не только в России, но и во всём мире. Он был избран членом Берлинской, Болонской, Парижской, Шведской академий, Лондонского королевского общества и др. В честь него в 1944 году была учреждена премия за лучшие исследования по математике (с 1997 года называется «Золотая медаль имени П. Л. Чебышёва»).

      Для Чебышёва не меньшее значение, чем конкретные научные результаты, всегда имела задача создания и развития российской математической школы. Чебышев продолжал учить своих учеников и по окончании ими университетского курса, направляя их первые шаги на научном поприще, путём бесед и драгоценных указаний на плодотворные вопросы. Чебышев создал школу русских математиков, из которых многие известны и в настоящее время. Его учениками были А.А.Марков, А.М.Ляпунов, Е.И.Золотарёв, А.Н.Коркин, Г.Ф.Вороной, Д.А.Граве, К.А.Поссе и др. Среди его последователей Ш.Эрмит, Г.Минковский, Н.Чеботарёв, А.Хинчин и др.

Чебышёв прожил всю жизнь один, он не женился и никто не знал почему. Детей он любил, беседовал об арифметике с детьми сестры, когда они приезжали к нему в гости в Петербург (муж сестры А. Тарасенков был известным врачом, лечил Гоголя, когда тот доживал последние дни).

Как и многие великие люди, Чебышёв был рассеян. Однажды, когда у него в доме сидели гости, он вдруг поднялся, сказал, что устал и что ему пора собираться домой. Вышел в переднюю и, к немалому удивлению гостей, стал одеваться.

П.Л.Чебышёв считается одним из основоположников теории приближения функций, основателем петербургской математической школы. Решением конкретных задач, касающихся соединения шарнирных механизмов, он значительно опередил своих современников. По существу П.Л.Чебышёв создал самостоятельную математическую науку о механизмах, поставив в ней такие проблемы, к решению которых наука стала подходить только в начале 20-го века.

"Сближение теории с практикой,- говорил Чебышёв,- даёт самые благотворные результаты, и не одна только практика от этого выигрывает, сами науки развиваются под влиянием её".

          Раз в неделю у П.Л.Чебышёва был приёмный день, когда двери его квартиры были открыты для каждого, кто хотел о чём - либо посоветоваться. Редко кто уходил, не обогатившись новыми мыслями. Чебышев на лекциях охотно раскрывал богатство своего духовного мира. Он иногда прерывал ход изложения, чтобы осветить своим слушателям историю того или иного факта. Такие отступления бывали довольно длительными. Чебышёв в таких случаях оставлял мел и доску, усаживался в особое кресло, стоявшее перед первым рядом слушателей. А в остальном ученики характеризовали его как педантически точного лектора, который никогда не пропускал лекции, никогда не опаздывал и никогда не задерживал аудиторию ни на минуту сверх положенного времени.

Сложным выкладкам он предпосылал разъяснение в самых общих чертах, а затем, молча и очень быстро, проводил доказательство. Но делал это он настолько подробно, что следить за ним было легко.

Профессор К. А. Поссе (1847 - 1927), вспоминая лекции Чебышёва, писал : «Всякой, сколько-нибудь сложной выкладке предпосылал разъяснение её цели и хода в общих чертах, а затем производил вычисления на доске, большею частью молча, представляя студентам следить за ним глазами, а не ухом. Во время лекции Чебышёв часто делал отступления от систематического изложения курса, сообщая свои взгляды и разговоры с другими математиками по затронутым на лекциях вопросам, и выяснял сравнительное значение и взаимную связь между различными вопросами математики. Эти отступления очень оживляли изложение, давали отдых напряжённому вниманию слушателей и возбуждали интерес к изучению предмета в более широких рамках».

Чебышёв не одобрял увлечения чтением текущей математической литературы. Он считал, что такое чтение неблагоприятно отражается на оригинальности собственных работ.

         Общественная деятельность Чебышёва не исчерпывалась его профессурой и участием в делах Академии наук. В качестве члена Учёного комитета Министерства просвещения он рецензировал учебники, составлял программы и инструкции для начальных и средних школ. Он проанализировал свыше 200 учебников по математике для средней школы, на которые дал обстоятельные отзывы.

        Чебышёв был одним из организаторов Московского математического общества и первого в России математического журнала — «Математический сборник».

         В течение сорока лет Чебышёв принимал активное участие в работе военного артиллерийского ведомства и работал над усовершенствованием дальнобойности и точности артиллерийской стрельбы. В курсах баллистики до наших дней сохранилась формула Чебышёва для вычисления дальности полёта снаряда. Своими трудами Чебышёв оказал большое влияние на развитие русской артиллерийской науки.

Больше половины своей жизни Чебышёв прожил в Петербурге, в казённой академической квартире. В конце ноября 1894 года П. Л. Чебышёв перенёс на ногах грипп - ложиться в постель он не привык, врачей он и раньше не жаловал - и вдруг занемог. Вечером 7 декабря 1894 г. на квартире у него были его младший брат генерал от артиллерии В.Л. Чебышёв и ученик Чебышёва академик А.А. Марков. Вечер прошёл в оживлённой дружеской беседе.

На следующий день он встал, оделся. Собирался набросать план работы с учениками, которые каждую неделю посещали его дом. Сам заварил чаю, налил стакан. В столовой никого не было. Через несколько минут прислуга, вошедшая в комнату, нашла его сидящим за столом, но уже мертвым. А стакан был горячий, и из него поднимался белёсый парок... В 9 часов 30 минут П.Л. Чебышев внезапно скончался от паралича сердца.

      П.Л.Чебышёв прожил 73 года. Его тело было перевезено в небольшое село Спас на Прогнаньи, что в 90 километрах южнее Москвы. В нём есть церковь, построенная предками Чебышёва. На северной стороне церковного двора похоронены отец и мать Чебышёва. Под колокольней в наглухо замурованном склепе погребены П. Л. Чебышёв и его два брата.

    С 1948 года восстановленные после войны склеп и часовня являются музеем П.Л. Чебышёва.

    Мозг Чебышёва хранится в Военно-медицинской академии в Санкт - Петербурге.

         Труды П.Л.Чебышёва были по достоинству оценены его современниками. Он был избран членом Петербургской (1853), Берлинской и Болонской академий, Парижской Академии наук (1860) (эту честь Чебышёв разделил лишь ещё с одним русским учёным, знаменитым Карлом Бэром, избранным в 1876 году и в том же году скончавшимся), членом-корреспондентом Лондонского Королевского общества, Шведской академии наук и др., всего 25 различных Академий и научных обществ. Чебышев состоял также почётным членом всех российских университетов.

        Он был награжден орденом Станислава I степени (1868 г.), орденом Анны I степени (1871 г.), орденом Владимира II степени (1876 г.), орденом Александра Невского (1883 г.), французским орденом Почётного легиона (1885 г.). У него был чин действительного тайного советника, который в «Табели о рангах» соответствовал чину полного генерала и должности министра.

Многочисленные труды почти во всех областях математики и прикладной механики создали Чебышёву славу одного из величайших математиков. За разносторонность, глубину исследований и математический талант Чебышёва называли "русским Гауссом".

          Именем П. Л. Чебышёва названы: хребет на Шпицбергене, кратер на Луне; астероид 2010 Чебышёв; математический журнал "Чебышёвский Сборник"; суперкомпьютер СКИФ МГУ «ЧЕБЫШЁВ»; многие объекты в современной математике. Раз в пять лет за выдающиеся результаты в области математики Российская академия наук присуждает Золотую медаль имени П. Л. Чебышёва.