Математический гений Индии

Национальный день математики в Индии ежегодно отмечается 22 декабря. Этот праздник провозгласил премьер-министр страны во время торжеств, посвященных 125-й годовщине рождения индийского математика Сринивасы Рамануджана Айенгора. Сринива́са (Шриниваса) — это часть родового имени, которая присваивается ребёнку по имени отца, Рамануджан — имя, Айенго́р — слово обозначающее касту брахманов.

        Сринивас Рамануджан Айенгар (Srinivasa Ramanujan Iyengor) родился 22 декабря 1887 года в доме своей бабушки в Эроде на юге Индии, небольшой деревне примерно в 400 км к юго-западу от Мадраса (штат Тамилнаду). Когда Рамануджану был один год, его семья переехала в город Кумбаконам, около 160 км от Мадраса (Ченная).

       Его родители принадлежали к привилегированной касте браминов, но жили бедно и ничем не отличались от окружавших их мелких служащих, торговцев и крестьян.

Отец Рамануджана был бухгалтером в маленькой текстильной лавке в городе Кумбаконаме Танджорского района Мадрасской провинции. Имеются сведения о том, что мать Рамануджана была незаурядной волевой женщиной; однако она находилась в плену узких кастовых и религиозных предрассудков.

Рамануджан почитал свою мать и находился в полном её подчинении. Она же, естественно, не была в состоянии понять внутренний мир своего сына и его непреодолимую тягу к математике. Действуя, как это часто бывает, из лучших побуждений, она тормозила его развитие и сильной рукой направляла его по единственно известному ей, традиционному в среде их семьи, жизненному пути мелкого служащего или чиновника. Только влечение гения помогло ему стать творческим математиком, свободно отдающимся занятиям любимой наукой. Но это произошло слишком поздно.

Рамануджан воспитывался в атмосфере понятной в условиях колониальной Индии враждебности ко всему европейскому и в особенности к английскому, причём в окружавшей его среде протест против колониального гнёта выражался в строгом соблюдении национальных обычаев, старого уклада жизни и традиционной браминской системы воспитания и образования.

 Естественно, что в отношении математического развития это ставило юного Рамануджана  в очень тяжёлые условия, наложившие сильный отпечаток на всю его научную карьеру. Следует также помнить, что британская администрация со своей стороны не прилагала особых усилий к выявлению народных талантов ни в какой области науки и искусства. Таким образом, самобытный гений Рамануджана в течение большей части его короткой жизни оставался предоставленным самому себе.

    Когда мальчику едва исполнилось 2 года он заболел оспой. Однако ему удалось оправиться от страшной болезни и выжить.

     Когда ему шёл пятый год, Рамануджан, как и все мальчики-брамины, был отдан в двухлетнюю школу, по окончании которой он поступил в начальную школу при городской средней школе Кумбаконама, где протекала вся его дальнейшая школьная жизнь. В 1897 г. он окончил начальную школу и занял первое место по результатам стипендиальных экзаменов в районном центре Танджоре, что дало ему право дальнейшего обучения в средней школе за половинную плату. Примерно к этому же времени относятся первые воспоминания о нём его сверстников и старших товарищей. В этих воспоминаниях он описывается как тихий задумчивый мальчик, редко участвующий в играх и шалостях своих одноклассников.

       Воспитанный в мистических традициях брахманизма, Рамануджан уже во втором классе средней школы (что соответствует примерно пятому классу нашей школы) задавал старшим товарищам и учителям вопрос о «высшей истине» в математике, так как привык считать, что в каждой области человеческой деятельности существует некая мистическая «высшая истина», первоначало вещей, управляющая данной областью и содержащая в себе всё, что может быть в ней известно. Говорят, что в ответ он получал указания на теорему Пифагора, или на проценты и учёт векселей.

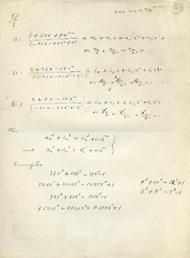
     Уже в четвёртом классе средней школы Рамануджан самостоятельно изучил полный курс тригонометрии по двухтомному руководству Лони (Loney), которое он одолжил у знакомого студента Мадрасского университета. Этот студент, как рассказывают, был поражён знаниями школьника по тригонометрии и часто обращался к Рамануджану за помощью в решении задач. В пятом классе Рамануджан самостоятельно открыл формулы Эйлера, выражающие синус и косинус через показательную функцию мнимого аргумента, но, узнав, что они уже известны, спрятал свои записи на чердаке дома. Это было его первое столкновение с западной математикой, из которого он понял, что учебник Лони содержит далеко не все известные математические факты. Однако бедность кумбаконамской библиотеки и плохие знания английского языка сильно затрудняли математическое развитие молодого Рамануджана.

         Только в 1903 г., когда Рамануджан был в шестом классе средней школы, ему удалось при помощи одного знакомого получить единственную книгу по высшей математике, имевшуюся в Кумбаконаме. Это была книга Карра «Сборник элементарных результатов чистой и прикладной математики» , изданная в двух томах в Лондоне в 1880, 1886 гг. Книга Карра содержит 6165 теорем и формул, большинство которых приводится без доказательств и выводов; конспективные доказательства намечены только для небольшого числа важнейших теорем.

      Двухтомник Карра, как и сотня других книг, был бы вскоре предан забвению, если бы не тот факт, что его читал Рамануджан. Это обстоятельство позднее повлекло за собой тщательнейшее рассмотрение этого учебника виднейшими математиками, пытавшимися установить, какие идеи Рамануджан мог почерпнуть из него и на какие мысли чтение Карра могло натолкнуть его.

Заинтересовала математиков и биография Карра. Джордж Шубридж Карр окончил Кембриджский университет и подвизался в Лондоне в качестве частного преподавателя математики. Он издал свой сборник в помощь своим ученикам-студентам. По отзыву Г.Х.Харди, книга Карра, которую нельзя назвать выдающейся, всё же имела несомненные достоинства, прежде всего систематичность подбора теорем и корректность их формулировок. Наряду с главами, посвящёнными элементарной алгебре, тригонометрии и аналитической геометрии, она содержала также главы по дифференциальному и интегральному исчислению, причём формальная сторона интегрального исчисления — в соответствии, по-видимому, с личными вкусами автора — была непропорционально подробно изложена и доведена до весьма сложных формул. Харди писал: «...Рамануджан сделал эту книгу знаменитой, и нет никакого сомнения в том, что она глубоко повлияла на него и явилась отправным пунктом его карьеры. Такая книга должна была иметь некоторые достоинства; и действительно, книга Карра... является не просто третьесортным учебником, а представляет собой книгу, написанную со знанием дела и с любовью к предмету...».

       Несколькими строками ниже Харди дал следующую заключительную оценку книги Карра: «В целом, если рассматривать её как пособие для мальчика с таким дарованием, книга Карра совсем не плоха, и восприятие Рамануджаном материала было изумительным».

        В составленном Харди в 1921 г. некрологе цитируется следующая выдержка из письма одного школьного товарища Рамануджана: «Он (Рамануджан) брал книгу Карра из библиотеки колледжа и с удовольствием выводил содержащиеся в ней формулы... Уже тогда он рассказывал товарищам о своих математических открытиях... Он обладал исключительной памятью и с лёгкостью цитировал полный список санскритских корней (atmanepada и parasmepada); он знал громадное число знаков в разложениях e , других чисел в десятичные дроби...».

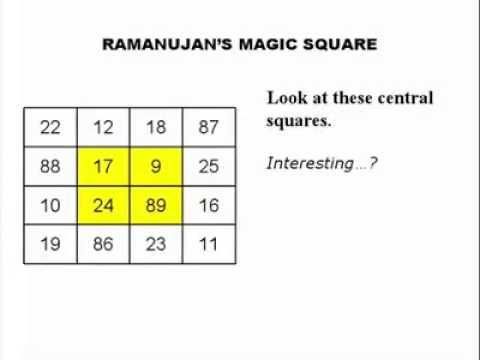
      Так как Рамануджан не мог пользоваться никакими другими книгами, то каждое найденное им доказательство являлось для него самостоятельным исследованием. Сначала он обратился к методам построения магических квадратов. Затем его внимание привлекла к себе геометрия; пытаясь решить задачу о квадратуре круга, он нашёл исключительно хорошую приближённую формулу для длины окружности, по которой длина земного экватора может быть вычислена с точностью до нескольких футов (1-2 метров).

       Вскоре он разочаровался в геометрии и, занявшись алгеброй, открыл несколько новых рядов. Рамануджан любил говорить, что формулы ему внушает во сне богиня Намаккаль. Интересно отметить, что он действительно часто, вставая по утрам с кровати, тут же записывал готовые формулы, после чего быстро проверял их; впрочем, строгие доказательства не всегда ему удавались. Все эти результаты он заносил в записную книжку, которую имел обыкновение показывать математикам, интересовавшимся его работой.

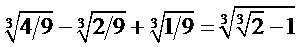
С 1914 по 1919 г. знаменитый математик Г.Х. Харди почти ежедневно встречался с Рамануджаном и беседовал с ним на всевозможные темы. В своих лекциях о Рамануджане Харди кратко касается основных этапов жизни Рамануджана и даёт свою оценку ему как человеку. Харди не утверждает, что Рамануджан был убеждённым атеистом, но цитирует высказывания самого Рамануджана, свидетельствующие о его равнодушии к вопросам религии. Однако Рамануджан соблюдал многочисленные условности индуистского ритуала, чтобы не огорчать своих религиозных родных и друзей. В частности, он был всю жизнь вегетарианцем и даже в последние два года своей жизни, когда вегетарианская диета тяжело сказывалась на его здоровье, не отказался от неё.

 Как и все аспекты личности Рамануджана, его религиозность и вообще отношение к религии были после его смерти предметом горячих споров. Харди отстаивал своё мнение о Рамануджане как о человеке высокоинтеллектуальном.  Харди считал, что по-настоящему разумный, интеллектуальный человек не может быть глубоко религиозным, как бы он внешне ни проявлял своё отношение к религии. Индийские друзья Рамануджана считали его истинно религиозным, а Харди слышал от него замечания совсем противоположного свойства.

 Шестой класс был последним классом средней школы. В 16 лет Рамануджан по окончании школы выдержал приёмные испытания в Мадрасский университет и в январе 1904 г. приступил к занятиям на первом курсе Кумбаконамского колледжа, входившего в состав Мадрасского университета. За свои первые успехи он получил специальную стипендию, предназначавшуюся для особо успевающих по английскому языку и математике. 

Однако вскоре его учебные дела в колледже пошли всё хуже и хуже, так как он отдавал всё время собственным математическим исследованиям, результаты которых он регулярно заносил в свои, ставшие впоследствии знаменитыми, записные книжки (они были полностью изданы в Индии в фоторепродукции только в 1957 г.). Он перестал выполнять задания, пропускал много занятий и в конце концов был оставлен на первом курсе.

     В жизни Рамануджана началась полоса неудач, длившаяся почти 10 лет. В течение 1905 г. он бродил по центральной Индии, затем вернулся в Кумбаконам, пытался продолжить учёбу в колледже, но не был допущен к занятиям, уехал в Мадрас, поступил там в 1906 г. в университет, но заболел и вновь вернулся домой в Кумбаконам. В 1907 г. он сделал попытку сдать экзамены за первые два курса университета экстерном, но провалился. После этого до 1909 г. он не имел определённых занятий, если не считать того, что всё это время Рамануджан неустанно занимался математикой, исписывая всё новые и новые страницы своих записных книжек.

       Когда ему исполнился 21 год, его мать соответственно обычаям тех времён договорилась о его свадьбе с десятилетней Янаки. Спустя ещё два года они начали жить вместе.

       В 1910 г. он обратился по поводу своего устройства на работу к индийскому математику Рамасвами Айару, основателю Индийского математического общества. Рамасвами Айар, просмотрев записные книжки Рамануджана, убедился в том, что имеет дело с человеком необычных способностей, хотя всей силы таланта Рамануджана он никак не подозревал. Он направил Рамануджана к Сешу Айару, который тогда был преподавателем Кумбаконамского колледжа и знал Рамануджана ещё как студента. Сешу Айар устроил Рамануджана на временную работу, но через несколько месяцев Рамануджан вновь остался без работы.

     Наконец, в декабре 1910 г. Рамануджану немного улыбнулось счастье: он был представлен влиятельному сановнику Рамачандра Рао, который сыграл важную роль в жизни Рамануджана. Однако улучшение положения Рамануджана заставило себя ждать ещё три года, когда Рамануджану был, наконец, подсказан самый важный шаг в его жизни: письмо к Харди в Кембридж.

    Рамачандра Рао был математиком только в том смысле, что имел университетское математическое образование; его административная деятельность не давала ему возможности творчески заниматься математикой. Но он был первым, кто распознал математический гений Рамануджана и, не задумываясь, употребил всё свое влияние для облегчения жизни и обеспечения научной карьеры Рамануджана.

      Рамачандра Рао сначала помогал Рамануджану из личных средств, а затем, видя, что Рамануджан тяготится таким положением, устроил его на работу в управление почт Мадраса с окладом 30 рупий в месяц. В почтовом ведомстве он работал с февраля 1912 г. по май 1913 г., когда его судьба, наконец, окончательно определилась благодаря вмешательству Харди.

        В 1911 г. в «Журнале Индийского математического общества» появились в печати первые задачи Рамануджана, сообщённые Сешу Айаром. Первая собственная статья Рамануджана появилась несколько позже в том же году. К 1912 г. установилась репутация Рамануджана как математика, во всяком случае на его родине. О нём знали уже некоторые работавшие в Индии англичане.

       К началу 1913 г. близкие к Рамануджану индийские математики настойчиво рекомендовали ему вынести свои результаты из записных книжек на более компетентный и строгий суд: послать их в центр математической мысли Британской империи — Кембриджский университет.

       До начала XX века Кембриджский университет не принадлежал к числу крупнейших мировых математических центров. Но в начале XX века молодые математики Г.Х. Харди и Д.И.Литлвуд подняли уровень математических исследований и математического образования в Кембридже.

Благодаря своей энергии и исключительной научной продуктивности, Харди уже в молодые годы стал известным учёным, возглавившим крупную математическую школу. Харди был всего на 9 лет старше Рамануджана, но он имел возможность приобщиться ко всей тысячелетней мировой математической культуре, тогда как Рамануджан имел в своём распоряжении только пару старых элементарных учебников и могучий математический гений.

Своё первое письмо к Харди Рамануджан написал 16 января 1913 г. Вот это замечательное письмо:

         К письму прилагались 120 сложных математических формул.

«Прилагаемые материалы» поразили Харди. По поводу этого первого и дальнейших писем Рамануджана Харди заметил: «...письма очевидным образом написаны не самим Рамануджаном, а по его просьбе каким-нибудь местным грамотеем, но — что самое важное — математические формулы в них несомненно принадлежали Рамануджану, и только ему одному».

       В завязавшейся между Рамануджаном и Харди переписке перед последним всё больше и больше раскрывался самобытный талант Рамануджана. В одном из последующих писем от 27 февраля 1913 г. Рамануджан писал:

«В Вас я нашёл друга, который с вниманием и пониманием относится к моим трудам. Это является стимулом для меня продолжить мои исследования... Во многих местах Вашего письма я нахожу указания на то, что требуются строгие доказательства, и Вы просите меня сообщить мои методы доказательств... Вот что я хочу Вам сказать: проверьте мои результаты, и если они совпадают с Вашими, то Вы должны по крайней мере согласиться с тем, что в моих основных рассуждениях имеется какое-то зерно истины... Чтобы сохранить мой мозг, мне нужна пища, и это является моей первой заботой. Одного Вашего письма с положительной оценкой моей работы будет достаточно для назначения мне стипендии от университета или от правительства...» В этом же письме мы находим следующее характерное место: «...Я сообщил ему, что по моей теории сумма бесконечного числа членов ряда 1 + 2 + 3 + 4 + ... равна –1/12. Если бы я сообщил этот результат сразу Вам, то Вы указали бы мне на сумасшедший дом как место, где мне надлежит быть...»

      Харди подозревал, что Рамануджан не хочет сообщить ему, английскому математику, свои методы и основные формулы. Поэтому он написал Рамануджану, что тот может ему всё сообщить без опасения, что Харди использует его методы. В письме от 17 апреля 1913 г. Рамануджан в ответ пишет: «...Ваше последнее письмо причинило мне боль... Я нисколько не опасаюсь того, что мои методы будут использованы другими. Напротив, я работаю моими методами уже 8 лет и не нашёл никого, кто бы понимал и оценил их. Как я уже писал в моём последнем письме, я нашёл в Вас внимательного и понимающего друга и готов передать в Ваше полное распоряжение те немногие результаты, которыми я располагаю. Только в силу новизны моих методов я не решаюсь даже сейчас сообщить Вам мой путь вывода тех формул, которые я Вам сообщил в моих предыдущих письмах...».

        В результате этой переписки Харди предпринял энергичные шаги по обеспечению Рамануджана стипендией и пригласил его приехать в Кембридж. Приглашение было передано Рамануджану через секретаря организации индийских студентов в Лондоне, но, хотя все финансовые вопросы благополучно разрешались, Рамануджан категорически отказался покинуть Индию; основную роль здесь сыграли кастовые предрассудки; особенно противилась поездке Рамануджана в Европу его мать. Оставалось только хлопотать о стипендии Рамануджану в самой Индии.

      Наряду с представлением Харди, к ректору Мадрасского университета по этому вопросу обратился также генеральный директор индийских обсерваторий Дж. Т. Уокер, который в своём ходатайстве, между прочим, писал: «...Имею честь обратить Ваше внимание на С. Рамануджана, клерка Мадрасского управления почт. Я с ним не знаком, но вчера мне в присутствии сэра Фрэнсиса Спринга показали его работы. Как мне сообщили, ему 22 года. Его работы произвели на меня сильное впечатление — они вполне сравнимы с работами членов Кембриджского университета... Я совершенно убеждён в том, что университет поступит разумно, если предоставит С. Рамануджану возможность заниматься математикой, не заботясь о заработке, хотя бы в течение нескольких лет...».

         В результате Мадрасский университет с 1 мая 1913 г. предоставил Рамануджану специальную стипендию в 75 рупий в месяц сроком на 2 года. Как отметил Харди, с этого дня Рамануджан стал математиком-профессионалом.

        Переписка не удовлетворяла Харди, и он продолжал настойчиво добиваться приезда Рамануджана в Кембридж как в интересах самого Рамануджана, за научную деятельность которого он себя чувствовал в известной мере ответственным, так и в интересах математики. Письменные увещевания Харди оставались безрезультатными, влияние матери на Рамануджана, по-видимому, перевешивало и мнение Харди, и советы многих друзей Рамануджана. Положение не изменилось до конца 1913 г. Но в самом начале 1914 г. в Мадрас по приглашению университета для чтения лекций прибыл один из кембриджских доцентов, ученик Харди, Э. Г. Нэвил (род. в 1889 г., впоследствии профессор университета). Нэвил имел поручение от Харди предпринять ещё одну попытку вывезти Рамануджана в Англию. По приезде в Мадрас Нэвил обратился в университет с меморандумом, в котором, в частности, писал:

     «Открытие гения Рамануджана обещает стать самым замечательным событием в математике нашего времени... Нельзя переоценить важности дальнейшего математического образования Рамануджана в одном из центров мировой науки, где он мог бы ознакомиться с более тонкими методами современной математики и работать под руководством учёных, знающих всё, что известно в данной области, и формулирующих те проблемы, в которых надо продолжать исследования... Я не вижу оснований сомневаться в том, что Рамануджан извлечёт максимальную пользу из общения с выдающимися западными математиками. В этом случае его имя станет одним из величайших в истории математики, а Мадрасский университет и город Мадрас будут гордиться тем, что способствовали его переходу от неизвестности к славе....».

       Вопрос о необходимости поездки Рамануджана в Кембридж широко и упорно дискутировался в кругах мадрасской интеллигенции, так что его мать, наконец, сдалась. Однажды утром она заявила, что во сне богиня приказала ей не противиться более отъезду сына и что она видела его сидящим в кругу европейцев в большом зале. Рамануджан получил от университета стипендию в 250 фунтов стерлингов в год на 2 года, оплату проезда в Англию и обратно, дорожные расходы и пр. Выделив из своей стипендии 60 рупий в месяц для матери, Рамануджан отбыл в Кембридж 17 марта 1914 г. В апреле он уже был зачислен в колледж Св.Троицы, где стипендия была увеличена ещё на 60 фунтов стерлингов.

Первые месяцы пребывания Рамануджана в Кембридже были посвящены восполнению основных пробелов в его математических знаниях. Харди, Литлвуд и другие кембриджские математики были изумлены как глубиной его знаний в одних вопросах, так и его полной неосведомлённостью в других.

В прохладных помещениях Тринити-колледжа Рамануджан согревался, только сидя у угольной печи. Он постоянно мёрз и простужался.

Вспоминая начало кембриджской карьеры Рамануджана, Харди писал: «Перед нами был человек, который мог оперировать с модулярными уравнениями и теоремами комплексного умножения неслыханно высоких порядков, чьё мастерство в области цепных дробей, во всяком случае с формальной стороны, было непревзойдённым, человек, самостоятельно открывший функциональное уравнение дзета-функции и главные члены асимптотики многих важнейших теоретико-числовых функций; в то же время он ничего не слышал о двояко-периодических функциях, не знал о существовании теоремы Коши и, вообще, имел только самое слабое представление о том, что такое функция комплексного переменного.

Его понимание сущности математического доказательства было более чем туманным; он пришёл ко всем своим результатам, как ранним, так и более поздним, как верным, так и неверным, при помощи странной смеси интуитивных догадок, индуктивных соображений и логических рассуждений...».

Предлагать такому человеку приступить к систематическому изучению основ математики было невозможно, но в одинаковой мере было невозможно, по выражению Харди, «дать ему шагать по жизни, думая, что все корни дзета-функции вещественны». В конце концов обучение Рамануджана пошло по пути собеседований и семинаров, где знания Рамануджана быстро пополнялись в процессе обсуждения нерешённых проблем и творческой работы. Через некоторое время Рамануджан прилично знал теорию функций и аналитическую теорию чисел. «Правда, он уже не стал, — говорит Харди, — математиком новой школы, о чём, быть может, и не стоит сожалеть, но он научился понимать, когда теорема доказана и когда она не доказана, а поток его оригинальных математических идей продолжал изливаться без малейших признаков истощения».

Война, разразившаяся осенью 1914 г., помешала продолжению образования Рамануджана. Литлвуд, который вместе с Харди вёл основную работу с Рамануджаном, был мобилизован, а, как сказал Харди, одного учителя для такого ученика было мало.

      Научная жизнь в Кембридже замерла, нарушились международные связи. Только на втором этаже внутреннего корпуса колледжа Св.Троицы, на стене которого висела под стеклом старая надпись «Посетителей просят не шуметь, так как это мешает занятиям достопочтенного сэра Исаака Ньютона», в квартире Харди продолжались ежедневные занятия с Рамануджаном.

Рамануджан упорно занимался математикой и только одной математикой. Он не проявлял ни малейшего интереса ни к каким другим областям, кроме как к анализу и теории чисел, ни тем более к другим точным наукам, политике, философии, литературе, спорту, которыми интересовался Харди. С камина в кабинете Харди на этих двух математиков безмолвно смотрели портреты Маркса, Эйнштейна и Хоббса (знаменитого английского игрока в крикет). В тех редких случаях, когда Харди удавалось вызвать Рамануджана на разговор на нематематические темы, Харди находил в нём довольно интересного собеседника.

        Про эти немногие минуты Харди писал: «...я хочу совершенно определённо заявить, что когда Рамануджан жил в Кембридже в хороших условиях и был здоров, он, несмотря на некоторые свои странности, был таким же нормальным и разумным человеком, как все другие кембриджские учёные, собиравшиеся за ужином в профессорской столовой. Не следует воздевать руки к небу и восклицать: «перед нами что-то непонятное, какое-то олицетворение извечной мудрости Востока!». Я не верю в извечную мудрость Востока, картина, которую я хочу нарисовать перед Вами, — это портрет человека, который имел свои особенности, как все выдающиеся люди, но в обществе которого Вы могли получить интеллектуальное удовольствие, с которым Вы могли за чашкой чая беседовать о политике или математике, короче, портрет не восточного чуда или одухотворённого идиота, а портрет умного человека, который, кроме того, был ещё великим математиком».