Математический гений Индии (Окончание)

(Окончание. Начало здесь ==>>)
Основная часть опубликованных работ Рамануджана была написана им в Кембридже самостоятельно или в соавторстве с Харди. Многие из этих работ Харди писал сам или подвергал английский текст Рамануджана редакционной переработке. Деятельное участие в их совместных занятиях принял также по возвращении с фронта Литлвуд.
Весной 1917 г. Рамануджан заболел и должен был лечь в Кембриджский госпиталь, где его регулярно посещали Харди и другие кембриджские математики.
Большую часть остального времени пребывания в Англии ему пришлось провести в больницах Лондона, куда он был вскоре переведён. Сначала его болезнь не вызывала особых опасений, но постепенно сырой английский климат, условия военного и послевоенного времени, а также недоверие Рамануджана к английским врачам и настойчивое соблюдение им неподходящей диеты окончательно подорвали его здоровье. Он имел от рождения слабые лёгкие, и его болезнь перешла в открытую форму туберкулёза. Рамануджану очень хотелось вернуться домой, в Индию. Но отъезд задерживался в течение двух лет в связи с его болезненным состоянием и трудностями морского сообщения (воздушного сообщения, конечно, ещё не существовало). Хотя в это время Рамануджан уже не мог так интенсивно заниматься математикой, как в первые три года его пребывания в Англии, он продолжал работать в больницах и санаториях.

После длительного отдыха осенью 1918 г. в одном из санаториев Уэльса на юго-западном побережье Англии его здоровье, как казалось, несколько улучшилось, и он с новой энергией взялся за работу.
26 ноября 1918 г. он был избран в члены Английского Королевского общества (Английская академия наук) и одновременно профессором Кембриджского университета. Он был первым индийцем, удостоенным этих почестей.
В начале 1919 г. здоровье Рамануджана настолько поправилось, что лучшие медицинские силы Англии считали его вне опасности, и он решил хотя бы на время вернуться в Мадрас, университет которого также приглашал его на работу. По-видимому, это была роковая ошибка, так как возможно, что оставаясь в Европе, он бы окончательно излечился. Но желание увидеться с родными и посетить родину после долгой разлуки взяло верх. Распрощавшись с Харди и своими кембриджскими друзьями, он в январе 1919 г. отправился в Индию. Что он был при том полон самых радужных надежд, видно из письма, которое он отправил ректору Мадрасского университета незадолго до своего отъезда: «11 января 1919 г.

СЭР, имею честь подтвердить получение Вашего письма от 9 декабря 1918 г. и выразить благодарность за оказываемую мне поддержку и предложенную честь.
Я считаю, однако, что оклад, установленный мне по прибытии в Индию, которое, как я надеюсь, произойдёт в самое ближайшее время, слишком велик по моим потребностям. Я думаю, что после оплаты моих расходов в Англии и помощи моим родителям в размере 50 фунтов стерлингов в год останется слишком большая сумма, часть которой я хотел бы использовать для благотворительных целей, таких, как снижение школьной платы за обучение бедных детей и сирот и как приобретение книг для школьных библиотек. Необходимые для этого шаги можно будет, конечно, предпринять после моего возвращения.
Я сожалею, что вследствие моей болезни я не мог за последние два года достаточно много заниматься математикой. Надеюсь, что скоро я буду в состоянии сделать больше и тем самым оправдать ту помощь, которую я получал.
Я остаюсь, Сэр, Ваш покорный слуга С.Рамануджан».
После отъезда Рамануджана Харди с нетерпением ждал от него вестей. Однако Рамануджан молчал в течение почти целого года. Наконец, в начале 1920 г. в Кембридж пришло последнее письмо Рамануджана:
«Мадрасский университет, 12 января 1920 г.
Я очень прошу меня извинить, что до сих пор не написал Вам ни одного письма... Я недавно открыл очень интересные функции, которые я называю «симулирующими» («mock») тета-функциями. В отличие от «псевдо»-J-функций (которые частично изучались проф. Роджерсом в его интересной работе), они входят в математику так же красиво, как обычные J-функции. Посылаю вам с этим письмом несколько примеров...»
В этом письме Рамануджан не сообщал о своём здоровье, и Харди решил, что оно по крайней мере удовлетворительно. В действительности же Рамануджан прибыл в Мадрас 2 апреля 1919 г. в очень плохом состоянии. По видимому, утомительная дорога окончательно подорвала его слабые силы. Он настолько исхудал, что друзья и родные с трудом узнали его.
Рамануджан провёл три месяца в Мадрасе, а затем отправился отдыхать в деревню, недалеко от селения Эрод, где он родился. Затем его перевезли в Кумбаконам, где прошла его юность и где он впервые познакомился с математикой. Силы его быстро угасали, но он не хотел лечиться и лихорадочно работал над своим последним детищем — симулирующими тета-функциями. До конца преданный математике Рамануджан создал замечательную работу, записанную в его так называемой «Потерянной тетради».

В январе 1920 г. под давлением друзей и врачей он переехал обратно в Мадрас, где ему оказывалась лучшая в городе медицинская помощь. Но спасти его было уже нельзя. 26 апреля 1920 г. Рамануджан умер в Чэтпуте — одном из предместий Мадраса.
К исполнению своих обязанностей профессора Мадрасского университета он фактически так и не приступил.
Существует только два портрета Рамануджана: фотография и один портрет маслом как члена Королевского общества, находящийся в колледже Св.Троицы в Кембридже. Харди, который лучше всех в Европе знал Рамануджана, считал, что этот портрет написан плохо и не передаёт правильного впечатления о внешности Рамануджана.

Весть о смерти Рамануджана была в Кембридже полной неожиданностью. Вскоре под руководством Харди началась интенсивная работа над научным наследством Рамануджана, начиная от самых ранних записей в его записных книжках и кончая симулирующими тета-функциями. Его записные книжки были от руки переписаны друзьями в Индии и присланы в Кембридж профессору Дж. Н. Ватсону, который взял на себя задачу их исчерпывающего анализа и занимался этим на протяжении нескольких лет.
Надо заметить, что, несмотря на пятилетнее общение с Рамануджаном, Харди так и не успел многого узнать от Рамануджана относительно его ранних результатов, путей, по которым он к ним пришёл, источника его знаний по некоторым вопросам, которые не освещены в книге Карра, и т.д. Конечно, впоследствии Харди очень сожалел об этом, но не мог себе поставить этого в вину, поскольку, как он говорил, было столько новых и животрепещущих вопросов, требующих неотложного обсуждения с Рамануджаном, что возврат к старым задачам всё откладывался и откладывался. Кроме того, Харди надеялся вновь встретиться с Рамануджаном, так как никто не мог ожидать столь быстрой его смерти.

Таким образом, многое в трудах Рамануджана так и осталось исторической загадкой. Вопросы приоритета Рамануджана никогда не интересовали, он искал математические истины, он был одержим страстью их познания, но источник этого познания его не особенно интересовал. У него не было книг, и он сам открывал эти истины. В научной честности Рамануджана Харди никогда не сомневался.

Харди начал работу над его научным наследством, пытаясь сохранить все его труды и открытия, которые содержались главным образом в письмах и записных книжках. Одна из этих книжек была надолго потеряна и найдена много лет спустя в 1976 году.
Индийскому ученому-самоучке принадлежит более 4000 теорем и уравнений, многие из которых он оставил недоказанными.

Если открытия Рамануджана в области математического анализа в какой-то незначительной мере базировались на упомянутой уже книге Карра, причём он проник в глубины анализа несоизмеримо дальше того уровня, на котором Карр излагал свой далеко не тривиальный материал, то в чрезвычайно сложной области аналитической теории чисел Рамануджан, по весьма аргументированному мнению Харди, не располагал вообще никакими пособиями. Рамануджан воссоздал эту обширную область математики, построенную европейскими учёными в течение столетий, совершенно самостоятельно — достижение, единственное в своём роде в истории математики.
При этом надо учесть, что, хотя Рамануджан и сформулировал несколько ошибочных теоретико-числовых теорем (из-за незнания некоторых очень тонких аналитических фактов, в частности того факта, что дзета-функция Римана имеет комплексные корни), он в то же время получил теоретико-числовые результаты, остававшиеся неизвестными европейским математикам XVIII и XIX веков!
Величие Рамануджана как математика и значимость его работ были оценены Харди и Литлвудом вскоре после его смерти. Харди писал: «Его проникновение в алгебраические формулы, преобразования бесконечных рядов и т.п. было просто поразительным. Я не знаю никого, кто мог бы в этом сравниться с ним, разве только Эйлер или Якоби. Он использовал, в значительно большей степени, чем современные математики, индуктивные и наводящие соображения; отправляющиеся от численных примеров. Хорошая память, терпение и виртуозность вычислителя сочетались в нём с силой обобщения, чувством формы и способностью мгновенной адаптации гипотез, которые производили исключительно сильное впечатление, и ставили его в области его собственных исследований выше всех современных ему математиков».

И Харди, и Литлвуд признавали, что во второй половине XIX века и в первых десятилетиях XX века имелось немало более значительных математиков, чем Рамануджан, но нельзя не присоединиться к их мнению, что в своей специальной сфере Рамануджан был недосягаем, «он был чемпионом каждой игры, правила которой он знал».

Через год после смерти Рамануджана Харди писал: «Можно расходиться во мнениях относительно значимости работ Рамануджана, критериев, с которыми следует подходить к нему как математику, и влияния, которое он окажет на развитие математики. Его работы не обладают той простотой и неизбежностью, которые характеризуют труды самых великих математиков; его результаты были бы значительней, если бы они не были столь необычными. Они отличаются, однако, одной неоспоримой чертой — глубокой и неуязвимой оригинальностью. Он стал бы наверно более крупным математиком, если был бы обуздан в молодости. Он открыл бы, вероятно, больше новых фактов, и притом большей значимости. С другой стороны, он был бы тогда в меньшей степени Рамануджаном и в большей степени европейским профессором, и трудно сказать, явилось бы это приобретением или потерей...».
Через 16 лет после того, как эти строки были написаны, Харди вновь вернулся к оценке Рамануджана уже с несколько более уравновешенных позиций и, процитировав приведённые выше свои высказывания, писал: «Всё, что я тогда сказал, я и сейчас готов повторить, за исключением лишь последней фразы, которая звучит как смешной сентиментализм.
Наука ничего не выиграла от того, что Кумбаконамский колледж отверг единственного большого учёного», которого он имел, и потеря была неизмеримой. Судьба Рамануджана — худший известный мне пример вреда, который может быть причинён малоэффективной и негибкой системой образования. Требовалось так мало, всего 60 фунтов стерлингов в год на протяжении 5 лет и эпизодического общения с людьми, имеющими настоящие знания и немного воображения, а мир получил бы ещё одного из величайших своих математиков...»
Именем Рамануджана названы:
• Гипотеза Рамануджана
• Суммы Рамануджана
• Функция Рамануджана
• Число Рамануджана — Харди
• Тождество Роджерса — Рамануджана
• Теорема Харди — Рамануджана
• Тождество Доугалла — Рамануджана
• Графы Рамануджана
Его жене на момент смерти мужа было всего 21 год, детей у них не было, но она так и не вышла замуж во второй раз. Она жила достаточно бедно, пока в 60-е годы Рамануджан не стал неким героем Индии, и ей стали выплачивать пенсии и награды. Оказывается, самое известное изображение Рамануджана – это фотография из его паспорта, которую она отдала одному из математиков-поклонников трудов индийского ученого. Она прожила на 73 года дольше мужа и умерла в 1994 году.
Рамануджан был первым индийским математиком, получившим мировое признание. В наши дни Республика Индия располагает значительными математическими кадрами, наука в Индии находится на большом подъёме. Труды Рамануджана до сих пор изучаются, а результаты исследований используются даже в областях совершенно далеких от математики – в компьютерном дизайне, полимерной химии и даже в изучении рака. Кроме того, современные учёные, в том числе и Стивен Хокинг, сделали вывод, что некоторые формулы Рамануджана объясняют поведение чёрных дыр.
Родни Дж. Бакстер из Австралийского национального университета признаёт, что открытия Рамануджана помогли ему решить некоторые задачи статистической физики, относящиеся к поведению системы взаимодействующих частиц, рассматриваемых как твердые шарики в гексагональной решётке наподобие медовых сотов. А Карлос Дж. Морено из Университета г. Нью-Йорка и Фримен Дж. Дайсон из Института высших исследований отметили, что физики начинают применять результаты Рамануджана в теории суперструн.
Память о Рамануджане живёт в сердцах индийских учёных, а имя его почитается как символ пробудившегося гения индийского народа.
Однажды он сказал:
- Для меня уравнение не имеет никакого смысла, если не выражает мысль Бога.
Рассказывают, что…
- Число π – отношение длины окружности к её диаметру – в 1987 г. было вычислено с беспрецедентной точностью: более ста миллионов десятичных знаков.
Тяга к вычислению π с миллионами десятичных знаков может показаться довольно бессмысленной, а само это занятие – лишь ареной для установления рекордов. Действительно, уже 39 знаков π достаточно для вычисления окружности, опоясывающей наблюдаемую Вселенную, с погрешностью, не превышающей радиуса атома водорода. Трудно вообразить физические ситуации, которые потребовали бы большей точности. Почему же математики и вычислители не удовлетворятся, скажем, 50 знаками π?
Этомy есть несколько причин. Во-первых, вычисление π стало чем-то вроде эталона: по нему оценивается совершенство и надежность применяемого компьютера. Вдобавок погоня за всё более точным значением π позволяет математикам проникнуть в таинственные и малодоступные закоулки теории чисел. Другая, более простая причина – «потому что оно всегда с нами». И в самом деле, π является неотъемлемой частью математической культуры вот уже более двух с половиной тысячелетий.
Кроме того, всегда есть шанс, что такие вычисления прольют свет на некоторые загадки, связанные с π. Ведь эта универсальная постоянная, несмотря на сравнительно простую природу, не так уж хорошо понята. Например, хотя и доказано, что π – трансцендентное иррациональное число, никому ещё не удалось доказать, что десятичные знаки π распределены случайно, т.е. каждая цифра от 0 до 9 появляется с одинаковой частотой.
Возможно, хотя и маловероятно, что, начиная с какого-то места, все остальные знаки π состоят только из 0 и 1 или проявляют какую-то другую закономерность. Более того,число π внезапно появляется в самых неожиданных задачах, не имеющих никакого отношения к окружностям. Так, допустим, что из множества целых чисел наугад выбирается какое-то число. Тогда вероятность того, что оно не имеет повторяющихся (кратных) простых делителей равна
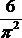
.
Как и многие другие выдающиеся математики, Рамануджан был пленён волшебной силой этого числа. Построенные недавно алгоритмы для вычисления π придали новый блеск математическим сокровищам, извлечённым благодаря возрождению интереса к работам Рамануджана. Однако большая часть того, что он сделал, всё ещё недоступна исследователям. Основные его работы содержатся в «Тетрадях», где он вёл личные записи, пользуясь собственной терминологией и обозначениями. Ещё огорчительнее для математиков, изучивших «Тетради» Рамануджана, то, что он обычно не записывал доказательств своих теорем. Расшифровка и редактирование «Тетрадей», предпринятые Брюсом К. Берндтом из Иллинойсского университета в Эрбана-Шампейн, только сейчас близятся к завершению.
По составленной Харди «шкале чистого таланта» для математиков Рамануджан получил 100 баллов, Литлвуд – 30, а себе Харди поставил 25. Немецкий математик Давид Гильберт, самая влиятельная фигура в математике того времени, заслужил только 80.
В течение пяти лет Харди и Рамануджан работали совместно в Тринити-Колледже Кембриджского университета. Сочетание блестящего мастерства Харди-аналитика и фантастической интуиции Рамануджана привело к необычайно плодотворному сотрудничеству. Они опубликовали серию основополагающих работ о свойствах различных теоретико-числовых функций, открывавших путь для ответа на вопросы типа: каково наиболее вероятное число простых делителей у данного целого числа? Сколькими способами можно выразить натуральное число в виде суммы меньших натуральных чисел?
Ставший кумиром молодых индийских интеллектуалов 32-летний Рамануджан умер 26 апреля 1920 г., как тогда думали, от туберкулёза, но, скорее, как считают теперь, от острого недостатка витаминов. (Это было в 1987 г. В 1994 г. произошёл новый поворот. Проанализировав симптомы и историю болезни Рамануджана Д. Янг поставил свой диагноз: гепатический амёбиаз.) Результаты Рамануджана, касающиеся числа π, связаны большей частью с его исследованиями модулярных уравнений – темы, наиболее подробно раскрытой в «Тетрадях».
Сриниваса Рамануджан, не имея специального математического образования, около ста лет назад был близок к доказательству оригинальными методами Великой теоремы Ферма (для случая n = 3). К такому выводу пришли учёные, изучившие предсмертные работы Рамануджана.
О числе 1729 (число Харди-Рамануджана) впервые сообщил британский математик Годфри Харди, который навещал Рамануджана в больнице. Ученый приехал на такси с номером 1729, который назвал скучным, о чем и сообщил индийцу. Рамануджан не согласился с британцем, сказав, что «это число — наименьшее натуральное число, представимое в виде суммы кубов двумя различными способами».
В настоящее время известно еще пять аналогичных чисел (представимых в виде суммы кубов). Самое малое из них Ta(1) = 2 = 13 + 13, а самое большое — Ta(6) = 24153319581254312065344 (оно представимо в виде суммы кубов шестью различными способами, например, Ta(6) = 387873 + 3657573). Ученые продолжают поиски таких чисел до сих пор.
Сегодня Рамануджан считается крупнейшим знатоком цепных дробей в истории математики. О Рамануджане сняли фильм «Человек, который познал бесконечность». Картина вышла в свет 17 сентября 2015 года. В память о великом человеке был снят фильм, рассказывающий о его жизни и деятельности: «Рамануджан».
В одном из интервью Харди сказал следующую фразу: «Каждое натуральное число было личным другом Рамануджана».
Сфера его математических интересов была очень широка. Это магические квадраты, квадратура круга, бесконечные ряды, гладкие числа, разбиения чисел, гипергеометрические функции, специальные суммы и функции, ныне носящие его имя, определённые интегралы, эллиптические и модулярные функции.
Чтобы сохранить наследие этого удивительного, ни на кого не похожего математика, в 1957 году в Институте фундаментальных исследований Тата была опубликована 2-томная книга с фотокопиями его черновиков.
Рамануджан обладал исключительной математической интуицией и мог своими уникальными методами обнаруживать самые неожиданные математические формулы, как "простые" арифметические

так и связанные с непрерывными дробями, крупнейшим в мире знатоком которых он считается до сих пор; например в письме к Харди он приводил следующие (недоказанные и сейчас?) замечательные математические тождества (1-е приводится с некоторыми изменениями):

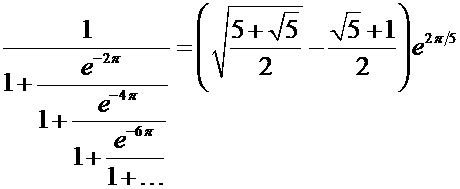

- Непрерывные дроби являются интересными математическими объектами. Известно, что все ирррациональные числа представляются непериодическими десятичными дробями, в то время как квадратичныые иррациональности (действительные корни квадратных уравнений с целыми коэффициентами) представляются периодическими непрерывными дробями, например:

Цифры в десятичных разложениях трансцендентных чисел e и π чередуются совершенно нерегулярным образом, но, как показал работавший долгое время в России швейцарский математик, механик, физик и астроном Леонард Эйлер (1707―1783), их разложения в непрерывные дроби имеют вполне регулярный вид:

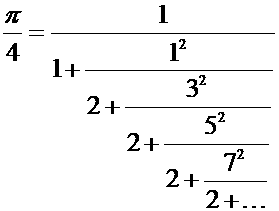
Современными математиками Рамануджан считается крупнейшим знатоком цепных дробей в мире. Одним из самых замечательных результатов Рамануджана в этой области является формула, в соответствии с которой сумма простого числового ряда с цепной дробью в точности равна выражению, в котором присутствует произведение е на
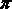
:
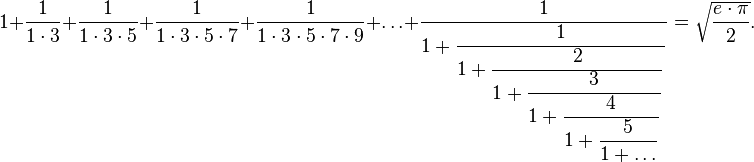
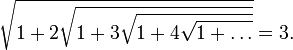
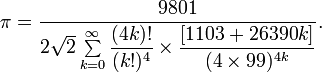
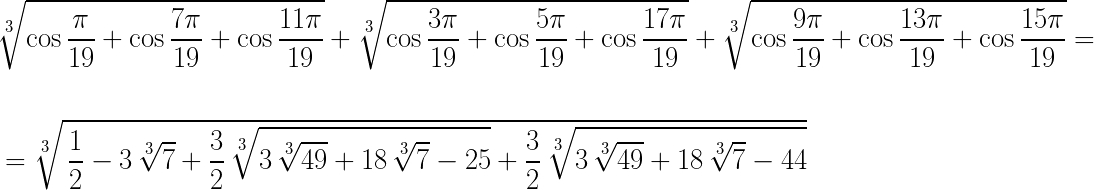
Бесконечные суммы, найденные Рамануджаном:
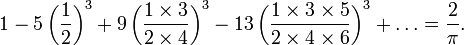

К моменту поступления в колледж Рамануджан хотел заниматься исключительно математикой, и в конце концов провалил все остальные экзамены и бежал, так что его маме даже пришлось писать в газету письмо с просьбой опубликовать сообщение о пропавшем сыне.
Харди, рождённый в семье школьных учителей, живших в 30 милях от Лондона, с детства был самым способным учеником -- в частности, особенно в сфере математики. Харди сначала перешёл в Винчестер, а затем и в Кембридж. После окончания образования Харди стал стипендиатом колледжа, и получил право на пожизненную стипендию. Это произошло в 1900 году. К 1913 году Харди оказался респектабельным и крайне успешным британским математиком.
Рамануджан сам провёл исследование и разработку чисел Бернулли, сумел вычислить постоянную Эйлера-Маскерони до 15 чисел после запятой.
29 декабря 2012 года учёные, наконец, решили 100-летний загадочный пазл, который описал на смертном одре Рамануджан, утверждая, что он явился ему во сне. В 1920 году на смертном одре Рамануджан написал письмо своему наставнику английскому математику Харди, в котором изложил ряд новых математических функций, о которых никто никогда не слышал раньше.
Машина Рамануджана (англ. Ramanujan Machine) — созданная группой израильских учёных из Техниона и тель-авивского отделения компании Google компьютерная программа, которая автоматически генерирует математические гипотезы для фундаментальных констант. О её создании было объявлено в июле 2019 года. Является программой, которая самостоятельно находит представления математических констант, например e и π, в виде бесконечных цепных дробей. Иными словами, это компьютерный алгоритм.
Харди остроумно прокомментировал результаты, сообщённые ему Рамануджаном: «Они должны быть истинными, поскольку если бы они не были истинными, то ни у кого не хватило бы воображения, чтобы изобрести их». Его формулы иногда всплывают в современнейших разделах науки, о которых в его время никто даже не догадывался.
