Творец небесной техники (Окончание)
Человек, который нашёл наше место в Солнечной системе

Поскольку Тихо Браге не опубликовал данных своих наблюдений, создавалось впечатление, что он ревниво охранял свои богатства. Кеплер писал: «Моё мнение о Тихо таково: он обладает несметными сокровищами, но не знает, как их следует употреблять, как это бывает у очень богатых людей. Следовательно, кто – то должен попытаться вырвать эти богатства у него».
Летом 1627 года Кеплер после 22 лет трудов, подводя итоги наблюдений Т.Браге, опубликовал (за свой счёт) астрономические таблицы, которые в честь императора назвал «Рудольфовыми». Спрос на них был огромен, так как все прежние таблицы давно разошлись с наблюдениями. Немаловажно, что труд впервые включал удобные для расчётов таблицы логарифмов. Кеплеровы таблицы служили астрономам и морякам вплоть до начала XIX века.

Кеплер дал математике толчок, после которого вычисления площадей и объёмов двинулись быстрыми темпами вперёд.
Достижения Кеплера в математике, астрономии, оптике не облегчили положения учёного: годами он хлопотал о выплате жалованья. Религиозные междоусобицы гнали его с места на место.

Замечательные математические способности Кеплера проявились при рассмотрении задач о вычислении объёмов. Он написал книгу "Новая стереометрия винных бочек" (1615). Описанный им способ вычисления объёмов содержит начала анализа бесконечно малых величин. Кеплер оригинальным способом нашёл объёмы 92-х тел вращения. В 1624 г. он составил таблицы логарифмов, похожие на современные.

Кеплер построил два правильных звёздчатых многогранника. Лишь спустя 200 лет С. Пуассону удалось указать существование ещё двух звёздчатых многогранников. Кеплеру принадлежит авторство на термин "среднее арифметическое".
Академик П.С. Александров описал следующий эпизод из жизни Кеплера, благодаря которому бывший уже до того времени великим астрономом Кеплер стал и великим математиком.
Примерно в 40 лет Кеплер овдовел и через два года решил жениться во второй раз. О своём намерении он информировал заинтересованных лиц. После того как отпали кандидатуры заведомо неприемлемые, на решающую встречу пришло 11 невест. Из них Кеплер выбрал одну, оказавшуюся
дочерью владельца винного погреба. Вскоре произошёл такой эпизод: пришёл торговец измерить объём проданного вина, находившегося в бочках. Для этого он опускал в каждую бочку железный прут, хотя бочки и не имели цилиндрической формы. Кеплер заинтересовался вычислением объёма бочек. В результате появилась уже упоминавшаяся гениальная работа, которая так и называется - "Новая стереометрия винных бочек". В этой работе на частном случае бочек Кеплер развил общие методы вычисления объёмов, ограниченных кривыми поверхностями, и стал, таким образом, одним из основателей интегрального исчисления, т.е. важнейшей части математического анализа.

Кроме того, Кеплер очень подробно проанализировал симметрию снежинок. Исследования по симметрии привели его к предположениям о плотной упаковке шаров, согласно которым наибольшая плотность упаковки достигается при пирамидальном упорядочивании шаров друг над другом. Математически доказать этот факт не удавалось на протяжении 400 лет — первое сообщение о доказательстве гипотезы Кеплера появилось лишь в 1998 году в работе математика Томаса Хейлса. Пионерские работы Кеплера в области симметрии нашли позже применение в кристаллографии и теории кодирования.
В ходе астрономических исследований Кеплер внёс вклад в теорию конических сечений. Кеплер вошёл и в историю проективной геометрии: он впервые ввёл важнейшее понятие бесконечно удалённой точки.
В 1604 году Кеплер издал содержательный трактат по оптике «Дополнения к Вителлию», а в 1611 году — ещё одну книгу, «Диоптрика». С этих трудов начинается история оптики как науки. В этих сочинениях Кеплер подробно излагает как геометрическую, так и физиологическую оптику. Он описывает преломление света, рефракцию и понятие оптического изображения, общую теорию линз и их систем. Вводит термины «оптическая ось» и «мениск», впервые формулирует закон падения освещённости обратно пропорционально квадрату расстояния до источника света. Впервые описывает явление полного внутреннего отражения света при переходе в менее плотную среду.

Описанный им физиологический механизм зрения, с современных позиций, принципиально верен. Кеплер выяснил роль хрусталика, верно описал причины близорукости и дальнозоркости.
Отношение Кеплера к астрологии было двойственным. С одной стороны, он допускал, что земное и небесное находятся в некоем гармоничном единстве и взаимосвязи. С другой — скептически оценивал возможность использовать эту гармонию для предсказания конкретных событий.

Кеплер говорил: «Люди ошибаются, думая, что от небесных светил зависят земные дела». Широко известно также другое его откровенное высказывание: "Конечно, эта астрология — глупая дочка, но, Боже мой, куда бы делась её мать, высокомудрая астрономия, если бы у неё не было глупенькой дочки! Свет ведь ещё гораздо глупее и так глуп, что для пользы этой старой разумной матери глупая дочка должна болтать и лгать. И жалованье математиков так ничтожно, что мать, наверное бы, голодала, если бы дочь ничего не зарабатывала". Тем не менее, Кеплер не порывал с астрологией никогда. Более того, он имел свой собственный взгляд на природу астрологии, чем выделялся среди астрологов-современников.
Вторая жена Кеплера, Сюзанна Рейттингер, была спокойной, доброй и трудолюбивой женщиной. Она с достоинством переносила лишения и невзгоды. А их на её долю выпало немало: забота о куске хлеба, жизнь на грани нищеты, смерть троих из семи родившихся детей. А в будущем её ожидала участь молодой вдовы с четырьмя малолетними детьми на руках без средств к существованию.

Кеплер верил, что тщательный математический анализ Тихо Браге, последнего великого астронома перед изобретением телескопа, позволит ему сделать окончательный вывод, какая теория планетарного движения верна: гелиоцентрическая теория Коперника, геоцентрическая теория Птолемея или теория, разработанная Тихо. Но после нескольких лет мучительных расчётов к своему смущению Кеплер обнаружил, что наблюдения Тихо не соответствуют ни одной из этих теорий.
Он понял, в чём заключалась проблема: Тихо Браге, Коперник и все остальные астрономы предполагали, что планетарные орбиты – круги. На самом же деле орбиты не круговые, а скорее эллиптические.
Кеплер не объяснил, почему планеты движутся по таким орбитам. Эту задачу позже решил И. Ньютон.
Вклад Кеплера в астрономию почти сравним с вкладом Коперника. Но Кеплер был более оригинален и преодолел огромные математические трудности.
Открытия Кеплера сыграли большую роль в формировании научной картины мира. Он по праву считается одним из творцов небесной механики. Опираясь на законы Кеплера, И. Ньютон открыл свой знаменитый закон всемирного тяготения. Уже современники Кеплера убедились в точности новых законов, хотя их глубинный смысл до Ньютона оставался непонятным. Никаких попыток реанимировать модель Птолемея или предложить иную систему движения, кроме гелиоцентрической, больше не предпринималось.

Взгляды Кеплера на устройство Вселенной за пределами Солнечной системы вытекали из его мистической философии. Солнце он полагал неподвижным, а сферу звёзд считал границей мира. В бесконечность Вселенной Кеплер не верил и в качестве аргумента предложил (1610) то, что позже получило название фотометрический парадокс: если число звёзд бесконечно, то в любом направлении взгляд наткнулся бы на звезду, и на небе не существовало бы тёмных участков.
Строго говоря, система мира Кеплера претендовала не только на выявление законов движения планет, но и на гораздо большее. Аналогично пифагорейцам, Кеплер считал мир реализацией некоторой числовой гармонии, одновременно геометрической и музыкальной

Последние годы жизни Кеплера были омрачены: Германия в это время погрузилась в хаос Тридцатилетней войны, и никто не мог избежать серьёзных трудностей. Главной проблемой Кеплера было его жалованье. Императоры неохотно платили даже в хорошие времена. Кеплеру задолжали большую сумму. Он был дважды женат и имел двенадцать детей. Поэтому финансовые трудности были для него действительно тяжёлыми.
В 1626 году в ходе Тридцатилетней войны Линц был осаждён и вскоре захвачен. Начинаются грабежи и пожары; в числе прочих сгорает типография. Толпа фанатиков осадила квартиру Кеплера и пыталась разграбить библиотеку «еретика и чернокнижника». Библиотека уцелела только потому, что его друзья, учёные-иезуиты, опечатали её якобы для дальнейшего расследования. Кеплер переезжает в Ульм.
В 1628 году Кеплер переходит на службу к Валленштейну. Пребывание в его свите далеко не соответствовало интересам пожилого учёного, всю жизнь посвятившего науке. Он покидает двор вельможи и возвращается в Линц, к семье. В 1630 году Кеплер отправляется к императору в Регенсбург, чтобы получить хотя бы часть жалованья. Чтобы уменьшить расходы, он поехал верхом (от Линца до Регенсбурга 150 км.). По дороге сильно простудился, проболел неделю в Регенсбурге и 5(15) ноября 1630 г. умер. Его похоронили друзья-почитатели, директор гимназии и пастор.
После смерти Кеплера наследникам досталось: поношенная одежда, 22 флорина наличными, 29000 флоринов невыплаченного жалованья, 27 опубликованных рукописей и множество неопубликованных; они позже были изданы в 22-томном сборнике.

Со смертью Кеплера его злоключения не закончились. В конце Тридцатилетней войны было полностью разрушено кладбище, где он похоронен, и от его могилы ничего не осталось. Часть архива Кеплера исчезла. В 1774 году бо́льшую часть архива (18 томов из 22) по рекомендации Леонарда Эйлера приобрела Петербургская Академия наук, сейчас хранится в Санкт-Петербургском филиале архива РАН. В Регенсбурге и в Вейле ему поставлены памятники.
Всю жизнь Кеплер посвятил обоснованию гелиоцентрической системы Коперника. Ему принадлежат пророческие слова: «Если найдутся корабли или паруса, приспособленные для небесных ветров, найдутся и те, кто не побоится даже такого простора. Поэтому давайте заложим основы астрономии для тех людей, которые появятся со дня на день, чтобы предпринять это путешествие».
Законы Кеплера получили объяснение в механике И. Ньютона.
Сам Кеплер считал своим главным достижением открытие мифической связи между орбитами планет и правильными многогранниками.
На могиле Кеплера была высечена надпись, составленная им самим:
Я измерил небеса,
землю теперь измеряю,
Дух воспарил в небеса,
тело распалось прахом.

В честь Кеплера названы один из лунных кратеров и малая планета № 1134.
Один из биографов Кеплера писал: «Он умер от истомления, печали и бедности 58 лет в Регенсбурге, в 1630 году». Человечеству он оставил три закона, на которых будет вечно покоиться планетарная астрономия.

Вся жизнь этого противоречивого, путаного и несчастного человека словно протестовала против того, чтобы он стал ученым, ни в каком начинании судьба не благоприятствовала ему. Недоносок, обреченный на гибель в день своего появления на свет, чудом выжил. Шестилетний мальчик, брошенный родителями в бреду оспы, снова победил свою слабую плоть. В 13 лет он умирал в третий раз и опять не умер: не мог он умереть, не совершив в этом мире предначертанного ему. Его родители словно специально вытравляли из него пытливость живого ума. Отец, этот почитавший себя дворянином грубиян, наемник, без славы пропавший под турецким ятаганом, все-таки успел вытащить семилетнего сына из школы и сделать служкой грязного кабака. Мать, темная женщина, нищее детство которой прошло у тетки, сожженной за колдовство, не умевшая ни читать, ни писать, хозяйка мокрой стойки в липком от дешевого вина фартуке,- что она могла дать этому нелюбимому болезненному существу?

Всю жизнь мучала его мозг гнусная мысль: «Как достать денег?» Всю жизнь словно шептала ему злая судьба: «Исчезни, утони в вине, налети на пьяный нож, умри», а он шёл, полз, продирался вперёд, яростно вколачивая солёные от слёз и скользкие от пота булыжники своих трудов, строил дорогу на космодром.»

А.Эйнштейн, назвавший Кеплера «несравненным человеком», писал о его судьбе: «Он жил в эпоху, когда ещё не было уверенности в существовании некоторой общей закономерности для всех явлений природы. Какой глубокой была у него вера в такую закономерность, если, работая в одиночестве, никем не поддерживаемый и непонятый, он на протяжении многих десятков лет черпал в ней силы для трудного и кропотливого эмпирического исследования движения планет и математических законов этого движения!»
Его именем названы астероид, кратер на Луне, космический грузовик и орбитальная космическая обсерватория, с помощью которой открыта новая планета, похожая по условиям на Землю и также названная именем Кеплера. Кеплер вывел “уравнение Кеплера”, используемое в астрономии для определения положения небесных тел. Кеплер предсказал существование двух спутников Марса и промежуточной планеты между Марсом и Юпитером.
В 1971 году к 400-летию со дня рождения Кеплера в ГДР была выпущена памятная монета достоинством 5 марок. В 2009 году к 400-летию открытия Кеплеровских законов в Германии выпущена памятная серебряная монета достоинством 10 евро.
Задача Кеплера

Доказать, что если взять три параллельные прямые l, m,n и пересечь их пучком прямых SА, SВ, SС пересекающих первую прямую l в точках А, В, С и через точки Е, F, Н пересечения со второй прямой m провести прямые, параллельные лучу SР, до пересечения с третьей прямой n в точках L, М, N, то прямые LА, МВ, NC, ЕР пересекутся в одной точке.
Однажды он сказал:
Главной целью всех исследований внешнего мира должно быть открытие рационального порядка и гармонии, которые бог ниспослал миру и открыл нам на языке математики.
Тем, кто слишком ограничен, чтобы понимать астрономическую науку, или слишком малодушен, чтобы без ущерба для своей
набожности верить Копернику, я могу лишь посоветовать покинуть школу астрономии ... Он может отречься от нашего движения в пространстве, вернуться домой и возделывать свой огород.

Я решительно предпочитаю острейшую критику одного умного человека бездумному одобрению толпы.
Глаз был сотворен, чтобы видеть цвета, ухо – чтобы слышать звуки, а человеческий разум – чтобы понимать.
Люди, откройте небесные силы. Познав их, вы сможете извлекать из них пользу.
Природа использует настолько мало всего необходимого ей, насколько это возможно.
Истина – дочь времени, и я не вижу ничего постыдного в том, чтобы быть ее акушером.
Природа, наделившая всякое животное средствами к существованию, дала
астрономии в качестве помощника и союзника астрологию.
Я могу подождать читателя сто лет, если Господь ждал зрителя пять тысяч.
Где материя, там геометрия.
Прежде, чем примириться с мыслью о чуде, надо попытаться применить любое другое объяснение; ведь с того момента как мы для объяснения прибегаем к идее сотворения, прекращается всякое научное объяснение.
Познавать означает сопоставлять воспринятое извне с внутренними идеями и выносить суждение о том, насколько то и другое совпадает.
Астрология — это всего лишь глупая дочь астрономии, и какая беда в том, что дочь кормит мать.
Люди ошибаются, думая, что от небесных светил зависят земные дела.
Рассказывают, что ...
Красивейшим проявлением гармонии является так называемое "золотое сечение" - особое разбиение отрезка, когда образуется изящная пропорция полученных частей. Настолько изящная, что математики Возрождения называли её "божественной". И. Кеплер писал: "Геометрия обладает двумя великими сокровищами - это теорема Пифагора, вторая - деление отрезка в среднем и крайнем соотношении. Первое можно сравнить с мерой золота, второе можно назвать драгоценным камнем".
- Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин a и b, при котором бо́льшая величина относится к меньшей так же как сумма величин к бо́льшей, то есть:
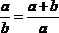
.
*Группа математиков под руководством профессора Питтсбургского университета Томаса Хейлса (Thomas Hales) представила положительные результаты проверки сделанного ранее доказательства математической гипотезы об упаковке шаров. Статья об этом опубликована в журнале Forum of Mathematics, Pi.
Гипотезу о наиболее плотном размещении шаров в пространстве высказал в 1611 году Иоганн Кеплер. Появление подобных задач в математике было вызвано практическими задачами по оптимальному размещению пушечных ядер. Согласно Кеплеру, среди всех упаковок шаров равного размера в трехмерном пространстве наибольшую среднюю плотность будет иметь гранецентрированная кубическая упаковка и упаковки, равные ей по плотности.
Профессор Хейлз и его ученик Сэм Фергюсон объявили о доказательстве гипотезы Кеплера в 1998 году, но решение было настолько длинным и сложным, что проверяющая его группа из двенадцати математиков работала пять лет и в итоге пришла к выводу, что доказательство «скорее всего, верно». «У них просто не было времени или сил, чтобы полностью проверить всё, – говорит редактор журнала Генри Кон. – Никаких непоправимых изъянов не было выявлено, но не удовлетворяла ситуация, когда доказательство, казалось бы, было недоступным для тщательной проверки математическим сообществом».
Тогда профессор Хейлз решил обратиться к компьютерам и использованию формальных методов проверки. Он и группа его соавторов изложили доказательство необычайно подробно, используя строгую формальную логику, а затем компьютерная программа проверила их рассуждения. В 2015 году Хейлз опубликовал препринт с результатами проверки, подтвердившими его правоту, а потом вышла официальная публикация в рецензируемом журнале. Доказательство гипотезы Кеплера стало самым сложным математическим доказательством, подтвержденным при помощи компьютера. Задачи об упаковки шаров имеют в наши дни практическое значение, о котором в XVII веке Кеплер не подозревал. Они помогают решить проблему передачи информации с сохранением передаваемого сигнала в условиях помех.
