Эмми Нётер – королева без короны

По мнению самых компетентных из ныне здравствующих математиков, госпожа Нётер была самым значительным творческим математическим гением (женского пола) из родившихся до сих пор.
Альберт Эйнштейн
Амалия Эмми Нётер (Amalie Emmy Noether) – выдающийся немецкий математик.
Эмми Нётер родилась 23 марта 1882 года в Эрлангене, была старшей из четверых детей в семье. Её родители, Макс Нётер и Ида Амалия Кауфман, происходили из состоятельных еврейских купеческих семейств.
Отец Эмми, Макс Нётер, преподавал математику в Эрлангенском университете. Его интеллект унаследовали сын Франц, посвятивший жизнь прикладной математике, и дочь Эмми, которая напоминала гадкого утёнка из сказки Андерсена — никто даже предположить не мог, каких научных высот она достигнет.

Вопреки распространённому мнению, «Эмми» — это не сокращённый вариант имени Амалия, а второе имя Нётер. Имя «Амалия» было ей дано в честь её матери и бабушки по отцовской линии. Но уже достаточно рано девочка отдала предпочтение второму имени, хотя в официальных документах она фигурирует как Амалия Эмми или Эмми Амалия. Эмми была очаровательным ребёнком, отличалась умом и дружелюбием. У Нётер была близорукость, и в детстве она немного шепелявила. В детстве Нётер посещала уроки игры на фортепьяно, в то время как большинство юных девушек обучались готовке и уборке. Но она не
Эмми испытывала страсти к этому виду деятельности, зато любила танцевать, поэтому она охотно посещала все торжества. При этом девушка не проявляла особого интереса к музыке, что отличает её от других математиков, которые часто любят музыку и даже играют на разных инструментах. Эмми исповедовала иудаизм — в то время это обстоятельство было несущественным, но в дальнейшем сказалось на её судьбе.
Обучение Эмми ничем не отличалось от обучения её сверстниц: она умела готовить и вести домашнее хозяйство, проявляла успехи в изучении французского и английского языков.
Первоначально Эмми планировала стать преподавателем английского и французского языков. С этой целью добилась разрешения посещать лекции в Эрлангенском университете вначале вольнослушательницей (1900), а с 1904 года, когда разрешили женское обучение, она была зачислена официально.

Однако в университете лекции по математике привлекали Эмми больше, чем любые другие. Она стала ученицей математика Пауля Гордана (1837-1912), под руководством которого защитила в 1907 году диссертацию по теории инвариантов. Она стала второй женщиной-доктором наук в Германии после Софьи Ковалевской.
Она часто вспоминала об этой диссертации в дальнейшем и всегда награждала её пренебрежительными эпитетами вроде „Formelngestrupp" и „Rechnerei". Однако уже в этой работе проявилось основное свойство её мате¬матического дарования: стремление к общим формулировкам математических проблем и уменье находить именно ту формулировку, в которой раскрывается подлинная логическая природа данного вопроса.
Уже в 1915 году Нётер внесла вклад в разработку общей теории относительности. Эйнштейн в письме к мировому лидеру математиков Давиду Гильберту выразил восхищение «проницательным математическим мышлением» Нётер.
В 1916 году Нётер переехала в Гёттинген, где знаменитые математики Давид Гильберт и Феликс Клейн продолжали работы по теории относительности, и знания Нётер в области теории инвариантов были им нужны. Гильберт оказал на Нётер огромное влияние, сделав её сторонницей аксиоматического метода.

Карьера Эмми Нетер является примером возмутительной косности и неспособности преодолеть предрассудки со стороны прусской академической и чиновной бюрократии.
Остроумный Гильберт нашёл способ преодолеть препятствия со стороны наиболее косных и консервативных преподавателей: он организовали курсы под своим именем, но на занятиях его всякий раз замещала Эмми, а недоброжелателям оставалось лишь скрежетать зубами.
Получение ею приват-доцентского звания в 1919 году произошло лишь вследствие настойчивости Гильберта и Клейна, после преодоления чрезвычайного сопротивления реакционных университетских кругов. Основным формальным отводом был пол кандидата: „Как можно допустить, чтобы женщина сделалась приват-доцентом: ведь, сделавшись приват-доцентом, она может стать профессором и членом Университетского сената; позволительно ли, чтобы женщина вошла в Сенат?" На это заявление последовала знаменитая реплика Гильберта: „Meine Herren, der Senat ist ja keine Badenanstalt, warum darf eine Frau nicht dorthin!" („Господа, ведь Сенат не бани, почему же женщина не может войти туда!")

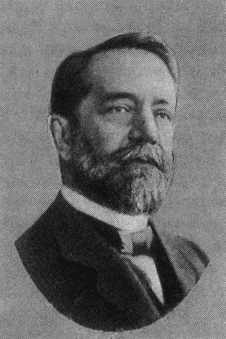
Начиная с 1832 года и до смерти Нётер в 1935 году, область математики, называемая алгеброй, претерпела глубокие изменения. Математики предыдущих столетий работали над практическими методами решения конкретных типов уравнений, например, кубических, а также над связанной с этим задачей построения правильных многоугольников с помощью циркуля и линейки. Начиная с работы Карла Фридриха Гаусса, доказавшего в 1832 году, что простые числа, такие как пять, могут быть разложены в произведение гауссовых целых чисел (комплексные числа, у которых как вещественная, так и мнимая часть целые числа), введения Эваристом Галуа понятия группы перестановок в 1832 году (по причине смерти, его работы были опубликованы лишь в 1846 году Лиувиллем), открытия кватернионов Уильямом Роуэном Гамильтоном в 1843 году и появления понятия абстрактной группы, предложенного Артура Кэли в 1854 году, исследования обратились к определению свойств более абстрактных и общих систем. Наиболее важный свой вклад в развитие математики Нётер внесла за счёт развития этой новой области, называемой абстрактной алгеброй.
Основные объекты абстрактной алгебры — это группы и кольца.
Группа состоит из множества элементов и одной бинарной операции, которая сопоставляет каждой упорядоченной паре элементов этого множества некоторый третий элемент. Операция должна удовлетворять определённым ограничениям — она должна обладать свойством ассоциативности, а также должен существовать нейтральный элемент, и для каждого элемента должен существовать обратный к нему элемент.

Кольцо, аналогично, имеет множество элементов, но теперь на нём определены две операции — сложение и умножение. Кольцо называется коммутативным, если операция умножения коммутативна (обычно также подразумевается её ассоциативность и существование единицы). Кольцо, в котором есть единичный элемент и каждый ненулевой элемент имеет обратный элемент относительно умножения (то есть элемент х, такой, что aх = ха = 1), называют телом. Поле определяется как коммутативное тело.
Группы часто изучают с помощью их представлений. В наиболее общем случае, представление группы G — это произвольное множество с действием группы G на этом множестве. Обычно множество является векторным пространством, а группа представляет симметрии этого пространства. Например, существует группа поворотов пространства относительно некоторой фиксированной точки. Поворот является симметрией пространства, потому что само пространство не изменяется при вращении, даже если положение объектов в нём изменяется. Нётер использовала подобные симметрии в своей работе по инвариантам в физике.
Мощный способ изучения колец — через модули над ними. Модуль над кольцом состоит из множества, как правило отличного от множества элементов кольца и называемого множеством элементов модуля, бинарной операции на множестве элементов модуля, а также операции, которая принимает элемент кольца и элемент модуля и возвращает элемент модуля. Понятие модуля является аналогом понятия представления для случая колец: забывание операции умножения в кольце сопоставляет модулю над этим кольцом представление группы. Реальной пользой от модулей является то, что изучение различных модулей над данным кольцом и их взаимодействий позволяет выявить структуру кольца, которая не видна при рассмотрении самого кольца.
Важным частным случаем этой структуры является алгебра. (Слово «алгебра» означает как раздел математики, так и один из объектов изучения в этом разделе.) Алгебра состоит из двух колец и операции, которая принимает по одному элементу из каждого кольца и возвращает элемент второго кольца, превращая второе кольцо в модуль над первым. Часто первое кольцо является полем.

Теоремы абстрактной алгебры являются мощными, поскольку они описывают многие системы. Талант Нётер заключался в том, чтобы определить максимальный набор свойств, которые являются следствиями данного набора, и обратно, определить минимальный набор свойств, которые отвечают за конкретные наблюдения. В отличие от большинства математиков, Нётер не получала абстракции путём обобщения известных примеров; скорее, она работала непосредственно с абстракциями.
Самый плодотворный период научной деятельности Нётер начинается около 1920 года, когда она создаёт целое новое направление в абстрактной алгебре. С 1922 года она работает профессором Гёттингенского университета, возглавляет авторитетную и быстро растущую научную школу.
Будь Эмма Нётер мужчиной, её, без всяких сомнений, приглашали бы на профессорские должности лучшие университеты страны. Ей же приходилось довольствоваться титулом «экстраординарный профессор» Гёттингенского университета, полученным ею 6 апреля 1922 года, когда ей исполнилось уже сорок лет. К этому времени она уже по праву считалась среди специалистов основоположником современной алгебры, ей удалось заложить краеугольные камни в фундаменты нескольких важнейших научных направлений. В указе о назначении Эммы Нётер на должность экстраординарного профессора специально оговаривалось, что никаких привилегий, предусмотренных государственным служащим, ей не положено.
Современники описывают Нётер как на редкость умную, обаятельную и приветливую женщину. Её женственность проявлялась не внешне, а в трогательной заботе об учениках, всегдашней готовности помочь им и коллегам. В числе её преданных друзей были учёные с мировым именем: Гильберт, Герман Вейль, Эдмунд Ландау, нидерландский математик Л. Брауэр, советские математики П.С. Александров, П.С. Урысон и многие другие.

В 1924–1925 годах школа Эмми Нётер сделала одно из самых блестящих своих приобретений: учеником её стал амстердамский студент Бартель Леендерт ван дер Варден. Ему шёл тогда 22-й год, и это было одно из самых ярких молодых математических дарований Европы. Ван дер Варден быстро овладел теориями Эмми Нётер, пополнил их существенными новыми результатами и как никто другой способствовал распространению идей Нётер в своей «Современной алгебре» 1930 года книге, ставшей каноном для нескольких поколений.
В абстрактную алгебру Нётер внесла решающую роль (наряду с Эмилем Артином и её учеником Б. Л. ван дер Варденом). Герман Вейль писал: «Значительная часть того, что составляет содержание второго тома «Современной алгебры» (Теперь просто «Алгебры») ван дер Вардена, должно принадлежать Эмми Нётер.»
Эмми Нётер нуждалась в попу¬ляризаторе своих идей: её лекции были рассчитаны на небольшой круг учеников, работающих в направлении её исследований и слушающих её постоянно. Они вовсе не были приспособлены для широкой математической аудитории: Эмми Нётер читала с внешней стороны плохо, торопливо и сбивчиво; но в них были громадная сила математической мысли и необыкновенное увлечение и горяч¬ность. Таковы же были и доклады ее в математических обществах и на съездах. Математику, уже владеющему её идеями и интересующемуся её работами, её до¬клады давали очень много; но математик, далеко стоящий от её работ, часто только с большим трудом мог понимать её изложение.
Курс общей теории идеалов, прочитанный ван дер Варденом в 1927 году в Гёттингене, имел громадный успех. Идеи Эмми Нётер в блестящем изложении ван дер Вардена покорили математическое общественное мнение сначала Гёттингена, а затем и других математических центров Европы.

В основном труды Нётер относятся к алгебре, где они способствовали созданию нового направления, известного под названием абстрактной алгебры. В эту область Нётер внесла решающий вклад (наряду с Эмилем Артином и её учеником ван дер Варденом).
Сама Нётер обычно скромно утверждала, что «es steht schon bei Dedekind» («это уже есть у Дедекинда»), и поощряла своих студентов убедиться самим, читая все дополнения Дедекинда. Таким образом, несмотря на чрезвычайно абстрактный характер алгебры Нётер, её студенты вынуждены были осознавать её непосредственное происхождение из теории чисел Гаусса и Дирихле. В «Алгебре» ван дер Вардена эта связь, к сожалению, нарушена, и многие из следующего поколения студентов выросли, не осознавая её. В последние годы происходит приятный перелом этой тенденции; в частности, в Алгебре сына Эмиля Артина, Майкла, теория чисел используется для иллюстрации теории идеалов.
Термины «нётерово кольцо», «нётеров модуль», теоремы о нормализации и теорема Ласкера-Нётер о разложении идеала теперь являются основополагающими.
В 1918 году была опубликована сенсационная теорема Нётер. Многие называли её именно так, хотя Эмма доказала немало и других теорем, в том числе очень важных. Нётер заслужила бы бессмертие, даже если бы умерла на следующий день после публикации теоремы. К сожалению, чтобы её объяснить понятным для читателя языком, пусть даже в упрощённом виде, нельзя обойтись без высшей математики и физики.

Если говорить просто, без символов и уравнений, то теорема Нётер в наиболее общей формулировке гласит:
Если физическая система обладает непрерывной симметрией, то в ней найдутся соответствующие величины, которые сохраняют значение с течением времени.
Понятие непрерывной симметрии в физике объясняется с помощью групп Ли. Если не углубляться в детали, то можно сказать, что в физике под симметрией понимают любое изменение физической системы, относительно которого физические величины в системы являются инвариантными. Это изменение посредством математически непрерывного преобразования должно затрагивать системы координат, а рассматриваемая величина до и после преобразования должна оставаться неизменной.
Эта теорема Эмми Нётер вызвала множество хвалебных отзывов, в том числе от Эйнштейна, который писал Гильберту: «Вчера я получил очень интересную статью госпожи Нётер о построении инвариантов. На меня производит впечатление то, что такие вещи можно рассматривать со столь общей точки зрения. Старой гвардии в Гёттингене не повредило бы, если бы её послали на обучение к госпоже Нётер. Похоже, она хорошо знает своё ремесло.»
Эта теорема, по мнению многих специалистов, является фундаментальной, а некоторые даже ставят её в один ряд с известной всем теоремой Пифагора.
По теореме Нётер, если в рамках нашей теории присутствует некая разновидность симметрии (предполагать подобное вполне разумно), то в системе будет сохраняться некоторая величина, которую можно измерить. Таким образом, можно определить, верна наша теория или нет.

На этом плодотворном подходе основана знаменитая серия книг «Теоретической физики» Ландау-Лифшица.
Важное значение имеет теорема Нётер в квантовой теории поля, где законы сохранения, вытекающие из существования определенной группы симметрии, обычно являются главным источником информации о свойствах исследуемых объектов.
Идеи и научные взгляды Нётер оказали огромное влияние на многих учёных, математиков и физиков. Она воспитала ряд учеников, которые стали учёными мирового класса и продолжили открытые Нётер новые направления.
Нётер придерживалась социал-демократических взглядов. На протяжении 10 лет жизни она сотрудничала с математиками СССР; в 1928–1929 учебном году она приезжала в СССР и читала лекции в Московском университете, где она оказала влияние на Л.С. Понтрягина и особенно на П.С. Александрова, до этого часто бывавшего в Гёттингене.
Современники описывают Нётер как не слишком красивую, но на редкость умную, обаятельную и приветливую женщину. Её женственность проявлялась не внешне, а в трогательной заботе об учениках. За Эмми повсюду следовала настоящая толпа учеников — шумных, недисциплинированных, но очень умных. То были «дети Нётер», которые внимали её словам. Они сопровождали её во время длинных прогулок и частых купаний в муниципальном бассейне, где Эмми плавала и ныряла, словно дельфин. Многие из «детей Нётер» впоследствии стали великими математиками благодаря идеям, которые они почерпнули от наставницы, хотя её педагогический дар был, если можно так сказать, нестандартным: она относилась к ученикам как курица-наседка к цыплятам — была неизменно строгой и требовательной и не отходила от них ни на шаг. Многим она напоминала скорее петуха, чем курицу, и они называли её, проявляя уважение к её уму и некоторую робость, в мужском роде — Der Noether.
С 1927 года влияние идей Эмми Нётер на современную математику всё время возрастает и параллельно возрастает и научная слава автора этих идей. Если в 1923–1925 годах ей приходилось доказывать важность развиваемых ею теорий, то в 1932 году, на международном математическом конгрессе в Цюрихе, её ждал блестящий успех. Нётер, совместно со своим учеником Эмилем Артином, получает премию Аккермана–Тёбнера за достижения в математике. Приз составил в денежном эквиваленте 500 рейхсмарок и является официальным признанием (хотя и с большой задержкой) её значительной работы в этой области. Прочитанный ею на этом съезде большой обзорный доклад был настоящим триумфом представляемого ею направления. Цюрихский конгресс был высшей точкой ее международного научного положения.
