ПЛОДОВИТЕЙШИЙ МАТЕМАТИК В ИСТОРИИ /Окончание/

Эйлера-математика нередко характеризуют как гениального «вычислителя». Действительно, он был непревзойдённым мастером формальных выкладок и преобразований, в его трудах многие математические формулы и символика впервые получают современный вид (например, ему принадлежат обозначения для е и π). Однако Эйлер был не только исключительной силы «вычислителем». Он внёс в науку ряд глубоких идей. Даже в тех вопросах, где он, как и другие математики 18 в., стоял на шаткой почве, его рассуждения, как правило, могут быть строго обоснованы и служат образцом глубины проникновения в предмет исследования.

           Эйлер умел показать, как основные законы механики, которые в предыдущем веке сформулировал И. Ньютон, можно применить в физических ситуациях. Например, применив законы Ньютона к движению жидкостей, он смог вывести уравнения гидродинамики. Аналогично он вывел ряд уравнений, которые полностью определяют движение твёрдого тела.

Эйлер применил свои таланты к решению астрономических задач, в особенности проблемы движения в условиях взаимного гравитационного притяжения Солнца, Земли и Луны. Полностью эта задача до сих пор ещё не решена.

Эйлер поддерживал волновую теорию света. Хотя сам он не открыл ни одного оригинального научного принципа, вклад его в науку, инженерное дело и математику огромен. Его великие трактаты "Введение в анализ бесконечно малых" (1748), ''Дифференциальное исчисление" (1755), "Интегральное исчисление" (1768-1770) сразу же стали классическими.

Около 60% работ Эйлера относятся к математике, остальные 40% - преимущественно к её приложениям. Невозможно перечислить все доныне употребляемые теоремы, методы, формулы, носящие его имя. Главным делом Эйлера как математика явилась разработка математического анализа. Работы Эйлера положили начало теории функций комплексного переменного. Он явился создателем вариационного исчисления, создал как самостоятельную дисциплину теорию обыкновенных дифференциальных уравнений и заложил основы теории уравнений с частными производными. Эйлер является основоположником теории специальных функций, им получены почти все классические разложения элементарных функций в бесконечные ряды и произведения. Он положил начало всем изысканиям, составляющим общую часть теории чисел, написав по этому вопросу свыше 100 мемуаров. Эйлер доказал ряд утверждений, высказанных П. Ферма, обобщил некоторые из них. При этом он открыл новые фундаментальные законы теории чисел, построил важные разделы её.

Эйлер обнаружил квадратичный закон взаимности, после чего стало возможным говорить о создании настоящей теории чисел. Последующие исследования Лежандра, Гаусса, Якоби были тесно связаны с этим законом. В 1950 г. И.Р.Шафаревич доказал общий закон взаимности для всех полей алгебраических чисел.

Эйлер является основоположником не только алгебраической, но и аналитической теории чисел. Отсюда ведут своё начало и работы по теории чисел в Литве. По замечанию П. Л. Чебышева, Эйлер положил начало всем изысканиям, составляющим общую часть теории чисел, к которой относится свыше 100 мемуаров.

В алгебре ему принадлежат результаты о решении в радикалах уравнений высших степеней. Он значительно продвинул аналитическую геометрию, заложил основы теории поверхностей. Он занимался и вопросами топологии, доказав важную теорему о выпуклых многогранниках. Эйлер положил начало теории гироскопов, внёс ценный вклад в теорию устойчивости, значительны его открытия в небесной механике. В оптике он дал формулу линзы, метод расчёта показателя преломления среды. Цикл работ он посвятил математической физике: задачам о колебании струны, пластинки, мембраны.

Во время пребывания в Берлине Эйлер говорил, что своими успехами в науках он обязан тому, что работал в Российской Академии наук. Мы должны сознаться, сколько обязаны благоприятным обстоятельствам, в которых только что находились. Что собственно меня касается, то в случае неимения такого превосходного случая я бы вынужден был главнейше прилежать к другим наукам, от которых, по всем признакам, я бы отупел только. Его королевское величество (Фридрих Прусский) недавно меня спрашивал, где я изучил то, что знаю. Я согласно истине ответил, что всем обязан своему пребыванию в Петербургской Академии наук".

            Эйлер хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики-математики (С. К. Котельников) и астрономы (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России. По отзывам современников, по характеру Эйлер был добродушен, незлобив, практически ни с кем не ссорился. К нему неизменно тепло относился даже Иоганн Бернулли, тяжёлый характер которого испытали на себе его брат Якоб и сын Даниил. Для полноты жизни Эйлеру требовалось только одно — возможность регулярного математического творчества. В то же время он был жизнерадостен, общителен, любил музыку, философские беседы.

           Эйлер был заботливым семьянином, охотно помогал коллегам и молодёжи, щедро делился с ними своими идеями. Известен случай, когда Эйлер задержал свои публикации по вариационному исчислению, чтобы молодой и никому тогда не известный Лагранж, независимо пришедший к тем же открытиям, смог опубликовать их первым. Лагранж всегда с восхищением относился к Эйлеру и как к математику, и как к человеку; он говорил: «Если вы действительно любите математику, читайте Эйлера».

     Эйлер активно трудился до последних дней. В списке его трудов около 860 названий. Труды Эйлера с большой пользой для себя изучали и «король математиков» Карл Фридрих Гаусс, и практически все знаменитые учёные XVIII—XIX веков. Заслуги Эйлера как крупнейшего учёного и организатора научных исследований получили высокую оценку ещё при его жизни. Помимо Петербургской и Берлинской академий, он состоял членом крупнейших научных обществ: Парижской АН, Лондонского королевского общества и т. д. В различных научных конкурсах работы Эйлера неоднократно удостаивались премий. Парижская академия наук 14 раз удостаивала премиями конкурсные работы Эйлера, выплатив ему в общей сложности 30 тыс. ливров. Большего числа премий не получал ни один учёный. За Эйлером следует Даниил Ι Бернулли, но он получил всего 10 премий.

  В сентябре 1783 года 76-летний учёный стал ощущать головные боли и слабость. 7 (18) сентября после обеда, проведённого в кругу семьи, беседуя с академиком А. И. Лекселем о недавно открытой планете Уран и её орбите, он внезапно почувствовал себя плохо. Эйлер успел произнести: «Я умираю», — и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг.

         Его похоронили рядом с первой женой на Смоленском лютеранском кладбище в Петербурге. Надпись на памятнике гласила: «Здесь покоятся бренные останки мудрого, справедливого, знаменитого Леонарда Эйлера».

     «Он перестал вычислять и жить», — сказал Кондорсе на траурном заседании Парижской Академии наук. 

      Могила затерялась и была найдена, в заброшенном состоянии, только в 1830 году. В 1837 году Академия наук заменила надгробную плиту новым гранитным надгробием (существующим и поныне) с надписью на латинском языке «Леонарду Эйлеру — Петербургская Академия»

         В 1955 году прах великого математика был перенесён в «Некрополь XVIII века» на Лазаревском кладбище Александро-Невской лавры по соседству с могилой Ломоносова.

         По выражению П. С. Лапласа, Эйлер явился учителем математиков 2-й половины 18 века. От его работ непосредственно отправлялись в разнообразных исследованиях П. С. Лаплас, Ж. Л. Лагранж, Г. Монж, А. М. Лежандр, К. Ф. Гаусс, позднее О. Коши, М. В. Остроградский, П. Л. Чебышев и др.

         В честь Эйлера названы: улица в Алма-Ате; кратер на Луне; астероид; Международный математический институт им. Леонарда Эйлера Российской Академии наук, основанный в 1988 году в Петербурге; благотворительный фонд поддержки отечественных учёных; Медаль, с 1993 года ежегодно присуждаемая канадским Институтом комбинаторики и её приложений за достижения в этой области математики; Золотая медаль имени Леонарда Эйлера Российской академии наук, ранее Академии наук СССР (Присуждается с 1991 года за выдающиеся результаты в области математики и физики).

        В 2007 году Центробанк РФ выпустил памятную монету в ознаменование 300-летия со дня рождения Леонарда Эйлера. Портрет Эйлера помещался также на швейцарскую 10-франковую банкноту и на почтовые марки Швейцарии, России и Германии. Имя Эйлера носят многие математические объекты.

        Дети математика так и остались в России. Старший сын, тоже талантливый математик и механик Иоганн Эйлер (1734–1800), как и обещала императрица Екатерина, был секретарем Императорской академии наук, которого сменил Фусс, а в 1826 году – сын Фусса, Павел Николаевич, так что организационной стороной жизни академии около ста лет ведали потомки Леонарда Эйлера.

     Младший, Христофор (1743–1808), дослужился до генерал-лейтенанта и командовал Сестрорецким оружейным заводом. Внук, Александр Христофорович (1773–1849) стал генералом от артиллерии, героем Отечественной войны 1812 года. Ещё один потомок, правда вернувшийся на родину предков, в Швецию, Ханс Карл Август Симон фон Эйлер-Хельпин (1873–1964) стал известным биохимиком, иностранным членом Академии Наук СССР, лауреатом Нобелевской премии по химии за 1929 год. Другую Нобелевскую премию, только уже в 1970 году, получил его сын, шведский биолог Ульф фон Ойлер (1905–1983).

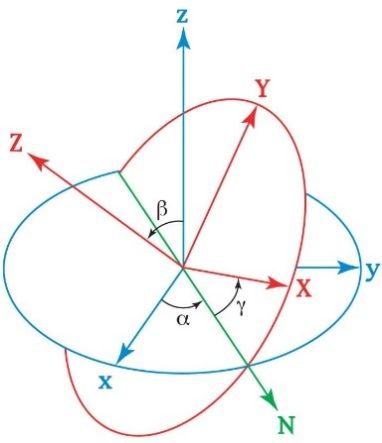
        Современная наука и технология развивались бы гораздо медленнее и были бы почти немыслимы без формул, уравнений и методов Эйлера. Одного взгляда на математические коэффициенты и учебники физики достаточно, чтобы увидеть ссылки на: углы Эйлера (движение твердого тела), постоянные Эйлера (ряды бесконечности), уравнения Эйлера (гидродинамика), уравнения движения Эйлера (динамика твердого тела), формулу Эйлера (сложные переменные), числа Эйлера (ряды бесконечности), многоугольные кривые Эйлера (дифференциальные уравнения), теорему однородных функций Эйлера (частичные дифференциальные уравнения), преобразования Эйлера (ряды бесконечности), закон Бернулли-Эйлера (теория упругости), формулы Эйлера-Фурье (тригонометрические ряды), уравнение Эйлера-Лагранжа (вычисление переменных, механика) и формулу Эйлера-Маклорена (цифровые методы). И здесь перечислены лишь самые важные примеры.

На родине Эйлера, в Швейцарии, в год празднования 200-летия со дня его рождения было решено издать полное собрание сочинений учёного. За 100 лет вышло около 80 томов, но работа ещё не завершена.

Задачи Эйлера

1. Каждое чётное число, начиная с четырех, можно разбить на сумму двух простых чисел.

2. Две крестьянки принесли на рынок 100 яиц, одна больше, нежели другая; обе выручили одинаковые суммы. Первая сказала второй : "Будь у меня твои яйца, я выручила бы 15 крейцеров". Вторая ответила: "А будь твои яйца у меня, я выручила бы за них 6⅔ крейцера". Сколько яиц было у каждой ?

3. Доказать, что в любом треугольнике точка пересечения медиан, точка пересечения высот (ортоцентр) и центр описанной окружности лежат на одной прямой (прямой Эйлера).

4. Доказать, что произведение двух чисел, из коих каждое есть сумма четырех квадратов, также равно сумме четырех квадратов.

5. Доказать, что во всяком четырехугольнике сумма квадратов сторон равна сумме квадратов его диагоналей, сложенной с учетверенным квадратом отрезка, соединяющего середины диагоналей.

6. Хозяин покупает лошадей и быков. За лошадь он платит 31 талер, а за быка - 21 талер. Сколько лошадей и сколько быков он купил, если израсходовал на покупку 1770 талеров.

7. Доказать, что середины сторон треугольника, основания высот и середины отрезков высот от вершин до точки их пересечения лежат на одной окружности (окружности Эйлера).

8. Пусть d - расстояние между центрами вписанной и описанной окружностей треугольника. Доказать, что d2 = R2 – 2Rr.

Однажды он сказал:

• Кто так превратно рассуждает в области математики, от того, наверное, мало оснований ждать чего либо толкового и в других науках.

• Математика, вероятно, никогда не достигла бы такой высокой степени совершенства, если бы древние не приложили столько усилий для изучения вопросов, которыми сегодня многие пренебрегают из-за их мнимой бесплодности. - Никто никогда столь успешно не проникал в тайны чисел, как Ферма.

• Именно математика в первую очередь защищает нас от обмана чувств. Одно дело – как на самом деле устроены предметы, воспринимаемые чувствами, другое дело – какими они кажутся – эта наука даёт надёжнейшие правила; кто им следует – тому не опасен и обман чувств.

Рассказывают, что...

• Степень магистра искусств Эйлер получил после блестящей речи о сравнении картезианской и ньютонианской философий. Вместе с ним такую же степень получил сын Иоганна Бернулли, тоже Иоганн, которому было 13 лет. Впоследствии он станет профессором и займёт кафедру отца в Базельском университете.

• В 1747 г. Шумахер, один из руководителей Академии, послал Л. Эйлеру на рецензию два сочинения М.В. Ломоносова, надеясь получить отрицательный отзыв и отстранить Ломоносова от научной деятельности. Ответ Эйлера разбил эти планы. Он писал : "Все сии сочинения не токмо хороши, но и превосходны, ибо он изъясняет физические и химические материи ... с таким основательством, что я совершенно уверен в справедливости его изъяснений".

• «Отчего вы не хотите говорить со мною?» - спросила в Берлине молчаливого и запуганного Эйлера мать короля Фридриха II. «Государыня, я прибыл из страны, где за слово вешают», - без улыбки ответил Эйлер.

• Маркиз Кондорсе рассказывал, что однажды два студента, выполняя независимо сложные астрономические вычисления, получили немного различающиеся результаты в 50-м знаке, и обратились к Эйлеру за помощью. Эйлер проделал те же вычисления в уме и указал правильный результат.

• А. С. Пушкин приводит романтический рассказ: якобы Эйлер составил гороскоп для новорождённого Иоанна Антоновича (1740), но результат его настолько испугал, что он никому не стал его показывать, и лишь после смерти несчастного царевича рассказал о нём графу К. Г. Разумовскому. Достоверность этого исторического анекдота крайне сомнительна.

• Рассказывают, что Эйлер не любил театр и, если попадал туда, поддавшись уговорам жены, то, чтобы не скучать, выполнял в уме сложные вычисления, подобрав их объём так, чтобы хватило как раз до конца представления.

• В эпоху парусного флота первостепенную роль играли количество, высота и расположение мачт на корабле. Парижская Академия наук объявила конкурс на оптимальное решение задачи. Поступило немало сочинений, и среди них – работа никому не известного юноши из Базеля, откуда «хоть три года скачи, ни до какого моря не доскачешь». Юношу звали Леонард Эйлер, а сочинение было его первой научной работой, получившей, кстати, «почётный отзыв». «Я не видел необходимости проверять разработанную мной теорию экспериментом,– писал впоследствии автор, который до того действительно никогда не видел моря.– Эта теория полностью выведена из неоспоримых принципов механики».

• В 1739 году вышла работа Эйлера по математической теории музыки. По поводу этой работы ходила шутка, что в ней слишком много музыки для математиков и слишком много математики для музыкантов. 
  

• Учёных - математиков (как тогда говорили - геометров) Фридрих II ценил гораздо меньше, чем заурядных литераторов. Он говорил, что слишком тяжело иметь на содержании сразу двух: Австрию и Геометрию. Даламбера он высоко ценил, так как тот был ещё и философом, но он не стеснялся посылать ему свои сатирические стихи против геометров, на что Даламбер отвечал мудрым молчанием. Эйлер же был для Фридриха предметом подшучивания. Например, он писал Вольтеру, что у его «одноглазого Геометра» (так он называл Эйлера), уши не созданы для понимания поэзии.
  

      * Учёными-секретарями Санкт-Петербургской Академии наук в течение целого века были потомки и родственники Эйлера. С 1769 года этот пост занимал Иоганн Альбрехт, после его смерти в 1800 г.– Н.Фусс, после его смерти – его сын Павел, правнук Эйлера.

Н.Фусс составил первую биографию Эйлера и подготовил к печати многие его работы. В конце жизни, получив на отзыв сочинение Н.И.Лобачевского по неевклидовой геометрии, не понял смысл открытия и дал резко отрицательный отзыв. Умер в 1826 году.

• Христиан Гольдбах (1690-1764), родившийся в Кёнигсберге и живший с 1742 г. в Москве и работавший в Министерстве иностранных дел, математикой занимался для удовольствия. С 1729 года и до самой смерти постоянно переписывался с Эйлером, главным образом по математическим проблемам. В одном из писем он высказал предположение, что каждое нечётное целое число, большее шести, может быть представлено суммой трёх простых чисел. В ответном письме Эйлер заметил: для этого достаточно, чтобы каждое чётное число можно было представить суммой двух простых чисел.

• Л. Эйлер был настолько плодовит, что и через 50 с лишним лет после его смерти его труды всё ещё печатались впервые.

• Академик П. П. Пекарский, опираясь на свидетельства современников Эйлера, так воссоздавал образ учёного: «У Эйлера было великое искусство не выставлять напоказ своей учёности, скрывать своё превосходство и быть на уровне всех и каждого. Всегда ровное расположение духа, весёлость кроткая и естественная, некоторая насмешливость с примесью добродушия, разговор наивный и шутливый — всё это делало беседу с ним столько же приятною, сколько и привлекательною».

• Как отмечают современники, Эйлер был очень религиозен. По словам Кондорсе, каждый вечер Эйлер собирал своих детей, слуг и учеников, живших с ним, для молитвы. Он читал им главу из Библии и иногда сопровождал чтение проповедью. В 1747 году Эйлер издал трактат в защиту христианства против атеизма «Защита божественного откровения от нападок свободомыслящих». Увлечение Эйлера теологическими рассуждениями стало причиной отрицательного отношения к нему (как философу) его знаменитых современников — Д’Аламбера и Лагранжа. Фридрих II, считавший себя «вольнодумцем» и переписывавшийся с Вольтером, говорил, что от Эйлера «попахивает попом».

     * Д’Аламбер в одном из своих писем к Лагранжу называет Эйлера «этот дьявол», как бы желая высказать этим, по мнению комментаторов, что сделанное Эйлером превышает человеческие силы.

• М. В. Остроградский заявил в письме Н. Н. Фуссу: «Эйлер создал современный анализ, один обогатил его более, чем все его последователи, вместе взятые, и сделал его могущественнейшим орудием человеческого разума». Академик С. И. Вавилов писал: «Вместе с Петром I и Ломоносовым, Эйлер стал добрым гением нашей Академии, определившим её славу, её крепость, её продуктивность».