КОРОЛЬ МАТЕМАТИКОВ
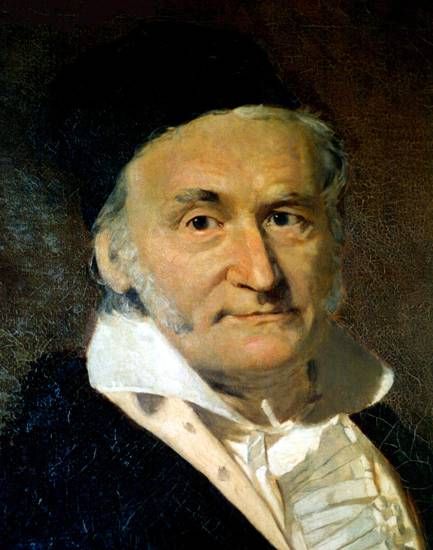
„Не считать ничего сделанным, если ещё кое-что осталось сделать”.
К.Ф.Гаусс
Карл Фридрих Гаусс (Carl Friedrich Gauß) родился в Брауншвейге 30 апреля 1777 года. Он был единственным сыном Гебхарда Гаусса и Доротеи Бенце (у его отца от предыдущего брака был ещё один сын).
Его дед был крестьянином. Отец Карла сначала работал слесарем, а потом стал садовником, совмещая это занятие с обязанностями счетовода в торговой конторе некоего купца. Мать Карла была дочерью каменщика; от природы она была женщиной умной, рассудительной, доброй и веселой. Карл был её единственным ребёнком, и она бесконечно и искренне любила его. Сын отвечал ей такой же горячей любовью. От матери он унаследовал рассудительность и мягкую натуру.
По словам биографов, Карл унаследовал от родных отца крепкое здоровье, а от родных матери яркий интеллект.
Однажды весной разлив резко поднял воду в канале, и игравший на его берегу Гаусс был смыт водой. Лишь благодаря счастливой случайности он не утонул.
Если составлять тройку великих математиков всех времён и народов, то это будут Архимед, Ньютон и Гаусс, которого называли "королём математиков".
Во всей истории математики нет никого, кого можно было бы сравнить с ним по ранней одарённости. Рассказывают такой случай. Однажды к отцу Карла собрались сослуживцы, чтобы распределить заработанные за неделю деньги. Здесь же был и трёхлетний Карл. Когда отец закончил расчеты, которые он проводил вслух, чтобы все слышали их, и объявил последствия, Карл воскликнул: "Папа, ты ошибся!" Присутствующие были поражены заявлением маленького ребёнка, но отец подсчитал всё сначала. Когда он назвал новую цифру (а раньше он действительно совершил ошибку), Карл воскликнул: "Теперь правильно!"
Позже он сам в шутку говорил: "Я научился считать раньше, чем разговаривать". Необыкновенные способности вычислять в уме были присущи ему всю жизнь. О десятилетнем Гауссе его школьный учитель говорил: "Он превзошёл меня, я ничему больше не могу его научить".

В 1784 г. Карла отдали в народную школу. Первые два года учёбы он ничем не отличался среди товарищей, его исключительные способности к арифметике проявились в третьем классе. Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: .
Истории о юных годах Гаусса рассказаны им самим уже в зрелом возрасте, поэтому есть основания полагать, что он был склонен несколько преувеличивать своё раннее развитие.
Молодой помощник учителя Мартин Бартельс обратил внимание герцога Брауншвейгского на одарённого мальчика и тот материально помог Гауссу. В 1791 году Карла в качестве одарённого молодого горожанина представили государю - герцогу Брауншвейгскому - и он стал бывать во дворе и развлекать придворных искусством счёта. Видимо, юноша произвёл впечатление на герцога: тот для начала пожаловал Гауссу стипендию в 10 талеров в год.
Судьба распорядилась так, что Бартельс в начале 19-го века приехал в Казань, и его учеником в Казанском университете был Н.И.Лобачевский.
Отец Гаусса был прямым, честным, грубоватым человеком. Резкость в общении с сыновьями у него иногда граничила с жестокостью. Карл был послушным и почтительным ребёнком. Он никогда не порицал отца, но никогда не питал к нему привязанности. Счастливая случайность спасла Гаусса от удела садовника или каменщика.
Карл был гордостью матери с его рождения (она родила его в 35 лет) до её смерти в 97 лет. Мать не разделяла намерения упрямого мужа оставить сына таким же невежественным, как он сам. Последние 22 года своей жизни мать провела в доме Карла. Гаусса мало беспокоила его слава, его успехами жила мать.

Гаусс был очень увлечён филологией, самостоятельно изучил классические языки, но влечение к математике победило. Ещё в Collegium Carolinum, куда он поступил в 1792 г., Гаусс начал те исследования по высшей арифметике, которые обессмертили его имя. Благодаря своим необыкновенным вычислительным способностям Гаусс переоткрыл "жемчужину арифметики" - "золотую теорему", к которой Л.Эйлер также пришёл индуктивно и которая известна как закон взаимности квадратичных вычетов (ряд утверждений, касающихся разрешимости квадратичного сравнения по модулю простого числа). Гаусс первым доказал эту теорему, ему было тогда только 19 лет. Произошло это более 200 лет тому назад.
В 1795-1798г.г. он учился в Гёттингенском университете, находящемся в государстве Ганновер, которым тогда управлял король Англии Георг ΙΙΙ, получая стипендию герцога Брауншвейгского. В качестве основания для переезда в Гёттинген Гаусс называл хорошую университетскую библиотеку.
Друзей у него было немного. Один из них -- Вольфганг (Фаркаш) Бойяи -- стал другом на всю жизнь. Сыну Вольфганга, Иоганну (Яношу), пришлось пройти практически тот же путь, которому следовал Гаусс, чтобы создать неевклидову геометрию в полном неведении того, что старый друг отца предвосхитил его.
О своих исследованиях построения правильного n-угольника, вписанного в круг, Гаусс сделал сообщение в печати: «Каждому, кто начинал изучать геометрию, известно, что возможно геометрическое построение различных правильных многоугольников, а именно треугольника, пятиугольника, пятнадцатиугольника, а также таких, которые получаются из них путём удвоения числа сторон. Всё это было известно ещё во времена Евклида; насколько я знаю, расширить этот перечень с тех пор не удавалось. Тем более заслуживает внимания сообщение, что возможно построение и других правильных многоугольников, например, семнадцатиугольника. Это открытие является частью ещё не законченной обширной теории, которая после её завершения будет опубликована.
К. Ф. Гаусс, студент-математик в Гёттингене».
Далее следовало примечание:
«Заслуживает внимания, что г-ну Гауссу всего 18 лет и что он занимается философией и классическим языкознанием с таким же успехом, как и математикой.
Э. А. В. Циммерман, профессор».
Это было признанием. Гаусс стал гордостью университета,- профессора и студенты превозносили его способности и успехи.
В 1796 году Гаусс доказал возможность построения с помощью циркуля и линейки правильного семнадцатиугольника. Он доказал, что уравнение:
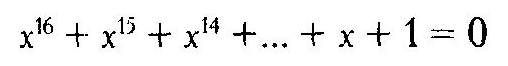
или уравнение
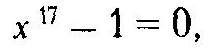
разрешимо в квадратичных радикалах.
Более того, он разрешил проблему построения правильных многоугольников до конца и нашёл критерий возможности построения правильного n-угольника с помощью циркуля и линейки: если n — простое число, то оно должно быть вида
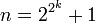
(числом Ферма).
«Математический век» Карла Гаусса — менее десяти лет. С 1796 года Гаусс ведёт краткий дневник своих открытий. Многое он, подобно Ньютону, не публиковал, хотя это были результаты исключительной важности (эллиптические функции, неевклидова геометрия и др.). Своим друзьям он пояснял, что публикует только те результаты, которыми доволен и считает завершёнными. Многие отложенные или заброшенные им идеи позже воскресли в трудах Абеля, Якоби, Коши, Лобачевского и др. Кватернионы он тоже открыл за 30 лет до Гамильтона (назвав их «мутациями»).

Все многочисленные опубликованные труды Гаусса содержат значительные результаты, сырых и проходных работ не было ни одной.
В 1799 году Гаусс впервые строго доказал основную теорему классической алгебры — возможность разложения любого многочлена с целыми коэффициентами на множители первой и второй степени с действительными коэффициентами (дальнейшее разложение квадратного трёхчлена с комплексными корнями считалось в те годы нецелесообразным). За это открытие Хельмштедский университет заочно присвоил Гауссу докторскую степень и предложил доцентуру.
Герцог Брауншвейгский продолжал опекать молодого гения. Он оплатил печатание его докторской диссертации (1799) и пожаловал неплохую стипендию. В своей докторской Гаусс впервые доказал основную теорему алгебры: всякое алгебраическое уравнение с вещественными коэффициентами имеет корень. До Гаусса было много попыток это сделать, наиболее близко к цели подошёл Д'Аламбер. Гаусс неоднократно возвращался к этой теореме и дал 4 различных её доказательства.

В Брауншвейг Гаусс вернулся в 1798 году и жил там до 1807 года. С наступлением нового века научные интересы Гаусса решительно сместились в сторону от чистой математики. Он много раз эпизодически будет обращаться к ней, и каждый раз получать результаты, достойные гения. В 1812 году он опубликовал работу о гипергеометрической функции. Широко известна заслуга Гаусса в геометрической интерпретации комплексных чисел.
С 1801г. Гаусс состоял приват-доцентом Брауншвейгского университета с месячным окладом в 8 талеров, что было явно недостаточно для безбедного существования. Академик Н.И. Фусс, ученик и друг Л. Эйлера, предложил Гауссу переехать в Петербург, пообещав ему избрание в академики. Гаусс принял предложение, но, как человек добросовестный, сказал, что сначала изучит русский язык, и начал им усиленно заниматься.
Через год Фусс повторил приглашение, но об этом узнал эрцгерцог Брауншвейгский и назначил Гауссу оклад в 400 талеров в год и повелел построить для учёного обсерваторию в Брауншвейге. Возникшая арифметическая задача оказалась для "короля математиков" совсем не простой. Он решает не ехать. В своём ответе Фуссу в 1802 г. он писал: "Однако я не вполне свободен. У меня есть обязанности, большие обязанности к нашему благородному государю".
В 1806 году герцог Брауншвейгский был ранен в бою и вскоре умер. Недостроенная обсерватория в ходе военных действий была разрушена. Гаусс с женой и маленьким ребенком остался без службы.
Смерть герцога, финансовые затруднения, потеря первой жены -- все это сказалось на здоровье Гаусса и сделало его жизнь несчастной в 30 лет с небольшим. Как и Декарт, в раннем детстве Гаусс испытал страх смерти, и всю жизнь потеря близких друзей наполняла его душу гнетущим чувством.
Наследственное предрасположение к ипохондрии, усугубленное непрестанным переутомлением, не улучшало дела. Он никогда не делился своими горестями с друзьями, для которых он всегда безмятежный корреспондент, но он доверился -- только однажды – рукописи, где научные рассуждения внезапно прерываются тщательно выписанными карандашом словами: «Смерть милее мне, чем такая жизнь». Его лекарством стала работа.
Он написал несколько писем в Санкт-Петербург, но из-за военных действий в Европе они не дошли. Лишь письмо, отправленное в конце 1807 года через ехавшего в Россию М. Бартельса, дошло до академии. Но в нём Гаусс уже сообщал, что принял приглашение Гёттингенского университета.
Выше других Гаусс ставил Ньютона, называя его "высочайший". Для Эйлера, Лапласа, Лагранжа, Лежандра у него был эпитет "яснейший".
Девизом Гаусса были строки из "Короля Лира" Шекспира:
„Ты, природа, моя богиня,
И я служу твоим законам ...”
Гаусс женился в 28 лет на дочери дубильщика Иоганне Остгоф. В 1804 году в письме своему другу Фаркашу Бойяи он писал о ней: "Прекрасное лицо мадонны, отражение спокойствия духа и здоровья, нежные, отчасти причудливые глаза, безупречная фигура – это одна сторона, яркий ум и развитой язык, это – другая, но спокойная, безмятежная, скромная и чистая душа ангела, который не может причинить вреда ни одному существу, - это лучшее". Осенью 1809г. Иоганна скончалась от послеродовых осложнений и через месяц умер новорожденный сын. Жена умерла, оставив ему троих детей. Это потрясение опустошило Гаусса, и он никогда уже не восстановил равновесия. Спустя год, ради своих маленьких детей Гаусс женится во второй раз, на дочери профессора Мине Вальдек. От этого брака у него было два сына и дочь.

Совместная жизнь Гаусса с Минной протекала довольно мирно, чего нельзя сказать о его отношениях с детьми, особенно от второго брака. Исключением стала только самая младшая дочь — Тереза, которая заботилась о Гауссе до его смерти. Старший сын учёного от первого брака, Иосиф, также поддерживал с отцом теплые отношения и даже помогал ему в некоторых работах. Будучи военным, Иосиф не очень часто общался с отцом, но Гаусс получал искреннее удовольствие от этого общения и гордился профессиональными успехами сына, о которых тот ему писал. Отношения с двумя сыновьями от Минны были ужасными, оба они, Ойген и Вильгельм, уехали в Северную Америку, спасаясь от семейных конфликтов. Ойген всегда упрекал Гаусса за то, что тот потребовал, чтобы сын занимался юриспруденцией, к которой сам Ойген не испытывал никакого интереса.

По рекомендации Александра фон Гумбольдта Гаусса назначают профессором в Гёттингене и директором Гёттингенской обсерватории. Эту должность он занимал до самой смерти.
В 1807 году наполеоновские войска занимают Гёттинген. Все граждане облагаются контрибуцией, в том числе огромную сумму — 2000 франков — требуется заплатить Гауссу. Это превосходило его возможности. Ольберс и Лаплас тут же приходят ему на помощь, считая для себя честью снять с плеч друга незаслуженное бремя. Но не в привычках Гаусса было принимать помощь, он отклоняет их деньги. Тогда неизвестный из Франкфурта присылает ему 1000 гульденов, и этот дар приходится принять. Только много позднее узнали, что неизвестным был курфюрст Майнцский, друг Гёте.
Первыми учениками Гаусса в Гёттингене были ставшие потом знаменитыми учёными и директорами обсерваторий Шумахер, Герлин, Николаи, Мёбиус, Струве, Энке.
Хотя Гаусс и считал преподавание потерей столь необходимого для научной работы времени, все отмечали высокое качество его лекций.
Гаусс был добрым, внимательным и отзывчивым человеком. Ученики боготворили его, преклонялись перед ним, относились к нему с почтением и любовью. Для исследований Гаусса характерна глубокая связь теоретических и прикладных вопросов, необычайная широта проблематики. Его работы оказали большое влияние на развитие высшей алгебры, теории чисел, дифференциальной геометрии, теории притяжения, классической теории электричества, геодезии, теоретической астрономии.

Первое крупное сочинение Гаусса по теории чисел и высшей алгебре - "Арифметические исследования" (1801) - во многом определило развитие этих дисциплин. Эту книгу называют первым величайшим шедевром Гаусса (ему было в это время 24 года). Арифметика была его первой любовью, в дальнейшем он всю жизнь сожалел, что не нашёл времени написать второй том этой книги, как замышлял в юности. Это сочинение поставило Гаусса в один ряд с Ферма, Эйлером, Лагранжем.
Книга «Арифметические исследования» содержала более 500 страниц большого формата, она была издана на средства герцога и ему посвящена. За пределами этой книги теорией чисел Гаусс, по существу, больше не занимался.
Книга состоит из семи глав, написанных столь сжато, что её называли "книгой за семью печатями". Лежен Дирихле был первым, кто вскрыл "семь печатей". Книга была быстро раскуплена, и даже любимый ученик Гаусса Эйзенштейн не имел своего экземпляра. А вот Дирихле повезло, экземпляр книги сопровождал его во всех путешествиях, он спал, положив книгу под подушку.

В этой книге Гаусс даёт обстоятельную теорию квадратичных вычетов, первое доказательство квадратичного закона взаимности - одной из центральных теорем теории чисел, даёт новое подробное изложение арифметической теории квадратичных форм, до того построенной Ж.Лагранжем. В конце книги, в 7-ой части, излагается теория уравнений деления круга (т.е. уравнений xn – 1 = 0), которая во многом была прообразом теории Галуа. Помимо общих методов решения этих уравнений, Гаусс установил связь между ними и построением правильных многоугольников. Он нашёл все те значения n, для которых правильный n - угольник можно построить циркулем и линейкой. В частности, решив это уравнение при n=17, он дал построение правильного 17-угольника при помощи циркуля и линейки. Гаусс придавал этому достижению очень большое значение и завещал выгравировать правильный 17-угольник, вписанный в круг, на своём надгробном памятнике, что и было исполнено.
По другим источникам на могильном камне Гаусса этого рисунка нет, но воздвигнутый ему в Брауншвейге памятник стоит на семнадцатиугольном постаменте.
Ещё Евклид решил задачи построения циркулем и линейкой правильных многоугольников с числом сторон 3, 4, 5, 6, 10 и 15. И было вообще не ясно: можно ли решить эту задачу для многоугольников с другим числом сторон, чем у Евклида? Результат Гаусса произвёл сенсацию. Основываясь на результатах Гаусса, Абель и Галуа смогли пойти дальше.

Следующие пять лет называют героическим периодом в творчестве Гаусса: на это время выпадает большая часть его величайших открытий в теории чисел, алгебре, математическом анализе. Тогда же он пришёл к идеям о неевклидовой геометрии.
Одна из самых удивительных сторон творчества Гаусса заключается в том, что он в своих первых работах практически не опирался на достижения предшественников, переоткрыв за короткий срок то, что было сделано в теории чисел за полтора века трудами крупнейших математиков.
Фундаментальные работы Гаусса по астрономии относятся к решению проблемы определения орбит малых планет, исследованию их возмущений. Как астроном, Гаусс получил широкую известность после разработки метода вычисления эллиптических орбит планет по трём наблюдениям, успешно применённого им к первым открытым малым планетам Церера (1801г.) и Паллада (1802г.). В связи с астрономическими исследованиями Гаусс изучал вопросы сходимости бесконечных рядов.
С открытием малой планеты Цереры связана такая история. Эту планету открыл Д. Пиацци. Но она была скрыта за плотными облаками, поэтому определить её точное местоположение не удалось. Гаусс за письменным столом (как говорят, «на кончике пера») вновь открыл Цереру. В письме к Пиацци Гаусс указал, где и когда можно наблюдать планету. Когда астрономы направили в указанную точку свои телескопы, они увидели Цереру.

«Слава Гаусса вполне заслуженна, и молодой 25 - летний человек идёт уже впереди всех современных математиков ...» - писали о нём.
Гаусс обладал железным характером. Выдающиеся способности сочетались у него с детской скромностью. В домашней обстановке он был строгим консерватором, не терпел никаких нововведений, был глубоко религиозным человеком, верил в загробную жизнь.
На протяжении всей жизни Гаусса обстановка его маленького кабинета свидетельствовала о скромных запросах хозяина. В кабинете были небольшой рабочий стол, конторка белого цвета, узкая софа и единственное кресло. В комнате была весьма умеренная температура, тускло горела свеча. Одет он был всегда в теплый халат и шапочку, был преимущественно спокойный и веселый. После напряженного труда Гаусс любил отдыхать: совершал прогулки, читал художественную литературу на немецком, английском и русском языках. Гаусс высоко оценивал русскую культуру и уважал талантливый русский народ. В России образованные круги, в свою очередь, высоко ценили Гаусса как ученого. Петербургская академия наук первой в мире выбрала Гаусса своим членом-корреспондентом.
В 1807г. он написал капитальный труд "Теория движения небесных тел". В книге был изложен метод наименьших квадратов, остающийся по сей день одним из самых распространённых методов обработки результатов наблюдений.
С этого периода он начинает читать в университете лекции по астрономии и становится директором обсерватории. Лишь в 30 лет Гаусс получил должность, которая позволяла ему содержать семью (жену и сына). Чтобы убедиться в силе своего метода вычисления орбит, Гаусс повторил вычисления орбиты кометы 1769 года, которую в своё время за три дня напряжённого труда вычислил Л. Эйлер, потерявший после этого зрение. Гауссу на это потребовался один час.

В 1810 году Гаусс получает премию Парижской академии наук и золотую медаль Лондонского королевского общества.
В письме к своему близкому другу Ф.В. Бесселю (1810) Гаусс писал: "Этой зимой я читал два курса лекций трём студентам, из которых один обладает средними знаниями, другой – менее чем средний, а третий лишён и знаний и способностей. Таковы тяготы профессии математика".
Имя Фридриха Вильгельма Бесселя достойно упоминания не только в связи с тем, что он был другом Гаусса.
Он родился 22 июля 1784 года в городе Миндене в Вестфалии (Германия) в семье мелкого чиновника. Гимназию Бессель бросил в 13 лет
из-за ненависти к зубрёжке латыни и продолжал образование дома под руководством отца. Обладая исключительно острым зрением, Бессель в 14 лет открыл визуально двойственность ε Лиры.
В 15 лет Бессель встал на самостоятельный трудовой путь: в 1799 г. он становится учеником конторщика в Бремене. Когда ему в 1805 г. предложили выгодную работу с хорошей зарплатой, он, по словам известного историка астрономии Агнессы Кларк, «предпочёл бедность и звёзды» и поступил ассистентом в обсерваторию.
Бессель обладал прирождённым математическим талантом и огромной работоспособностью. В письме брату он писал, что «математика - самая увлекательная наука из всех наук. Вместе с астрономией она заменяет мне ... развлечения, которые я знаю только по имени».
Труднейшую «Небесную механику» Лапласа и высшую математику он изучал лишь в свободные от работы утренние и ночные часы.
В 1804 г. Бессель вычислил элементы орбиты кометы Галлея и стал известен в научном мире. С этого времени ведёт отсчёт и его дружба с К. Гауссом.

В 1809 году Бесселю было предложено создать и возглавить вторую в Германии обсерваторию в Кёнигсберге (первая была открыта в 1705 г. в Берлине). С 1810 г. он - профессор математики и астрономии в Кёнигсбергском университете. Здесь он проработал до конца жизни.
Полная реорганизация Бесселем астрономических наблюдений позволила повысить их точность в 10 раз. Помимо астрономии он внёс значительный вклад в геодезию. В историю науки он вошёл как один из крупных математиков. «Функции Бесселя» и дифференциальное «уравнение Бесселя» нашли широкое применение в теоретической физике.
Умер Ф.В. Бессель 17 марта 1846 года в Кёнигсберге и был похоронен близ обсерватории. Его именем назван кратер на видимой стороне Луны.
Гаусса привлекала английская литература. Он читал романы Вальтера Скотта, как только они выходили в свет. Особое удовольствие доставляли ему исторические труды на английском языке. К Байрону же он питал почти неприязнь. Его любимым немецким поэтом был Жан Поль, а вот Гёте и Шиллера он ценил не очень высоко.
Занявшись геодезией (Гауссу было поручено провести геодезическую съёмку и составить карту Ганноверского королевства), он создал новую для того времени область геометрии — общую теорию поверхностей. Специально выделенные офицеры (и среди них сын К. Ф. Гаусса — Иозеф) вели измерения на местности с помощью сконструированного Гауссом гелиотропа. Сам Гаусс выполнял многочисленные вычисления.
Первоначально измерения делались с большими погрешностями, однако Гаусс настоял на уточнении триангуляции и добился небывалой по тем временам точности: сумма углов любого треугольника могла отличаться от 180 градусов не более чем на 2 угловых секунды! Титаническая работа закончилась лишь в 1848 году — географические координаты всех 2578 тригонометрических пунктов Ганноверского королевства были определены весьма точно.
«Я прихожу к убеждению, что геометрия не может быть доказана, по крайней мере человеческим рассудком и для человеческого рассудка, — писал Гаусс в 1817 году. — Может быть, в другой жизни мы придём к другим взглядам на природу пространства, которые нам теперь недоступны...»
Гаусс с удовлетворением воспринял открытие Лобачевского, которое соответствовало его внутренним убеждениям. Он высоко оценил достижение русского учёного и добился избрания его в члены-корреспонденты Гёттингенского учёного Королевского общества. Однако сам Гаусс никогда не выступал официально, а тем более в печати с признанием неевклидовой геометрии или со своими соображениями о ней.
Отрывки из писем Гаусса позволяют понять причины, по которым он не считал возможным объявлять не только о своих идеях (эти идеи Гаусс так и не разработал с достаточной чёткостью), но и о своём отношении к возможности «новой» геометрии. «Осы, гнездо которых вы разрушаете, подымутся над вашей головой»,— писал Гаусс в 1818 году ученику и другу, который собирался в новом издании своей книги выразить сомнение в справедливости пятого постулата.
«Если бы неевклидова геометрия была истинной…, мы имели бы a priori абсолютную меру длины,— писал он в 1824 году.— Но вы должны смотреть на это как на частное сообщение, которое не должно быть опубликовано».
«Вероятно, я ещё не скоро смогу обработать свои исследования, чтобы их можно было опубликовать. Возможно даже, что я не решусь на это всю свою жизнь, потому что боюсь крика беотийцев»,— писал Гаусс в 1829 году, через 3 года после того, как Лобачевский публично объявил о своём открытии.
Материалы дневника Гаусса позволяют утверждать, что он пришёл к мысли о возможности построения наряду с евклидовой геометрией и геометрии неевклидовой в 1818г., но из опасений быть непонятым не опубликовал эти результаты. Он колебался между желанием поддержать научную истину и опасностью растревожить осиное гнездо непонимающих.
В 20 - ые годы велись переговоры о переезде Гаусса в Берлин, где ему предлагали должность директора института. Переговоры затянулись на четыре года. Разногласия сводились к тому, должен ли будет Гаусс читать лекции, и сколько ему должны платить: 1200 или 2000 талеров в год. Переговоры провалились, но в Гёттингене Гауссу стали платить жалованье, на которое он претендовал в Берлине.
Непреходящее значение для всех наук, имеющих дело с обработкой наблюдений, имеют разработанные Гауссом методы получения наиболее вероятных значений измеряемых величин. Особенно широкую известность получил созданный Гауссом в 1821-1823 гг. метод наименьших квадратов (математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных). Гауссом заложены также и основы теории ошибок.
В 1824 году Гаусс был избран иностранным почётным членом Петербургской Академии наук. Современники отмечали тот факт, что Гаусс, став знаменитым, никогда не читал трудов других математиков: обычно он знакомился с концепцией и сам старался её либо доказать, либо опровергнуть. Труд Лобачевского стал исключением.
Гаусс заложил основы теории построения изображения в системах линз.
Гаусс свободно владел латынью, французским, английским. Он с удовольствием читал в оригинале произведения Диккенса, Свифта, Ричардсона, Мильтона, великих французских просветителей — Монтеня, Руссо, Кондорсе, Вольтера. Два младших сына Гаусса эмигрировали в США — и Гаусс заинтересовался американской литературой. Гаусс читал по-датски, шведски, испански, итальянски. В юности немного изучал русский, в 63-летнем возрасте, желая более подробно ознакомиться с работами Лобачевского, начал интенсивно заниматься русским языком. «Стал бегло читать по-русски и получал от этого большое удовольствие», — писал он одному из своих учеников. В личной библиотеке Гаусса впоследствии было обнаружено 57 книг на русском языке, и в том числе восьмитомник Пушкина.
(Окончание следует)
