Из истории теории чисел

Теория чисел, или высшая арифметика — раздел чистой математики, изучающий свойства натуральных и целых чисел.

       В первую очередь в теории чисел ставятся и решаются те проблемы, которые важны для математики и вычислительной науки в целом, представлявляются исторически важными, — порой настолько, что за решение сразу выдают премию и награды. Главной из таких проблем, наверное, остаётся проверка гипотезы Римана (1859 год) о распределении простых чисел.

      Теорию чисел могут условно разбивать на разделы:

• Элементарная теория чисел, изучающая элементарные связи и свойства чисел, сравнения, неопределённые уравнения.

• Алгебраическая теория чисел, изучающая алгебраические числа и их применения к решению задач, связанных с натуральными или целыми числами.

• Аналитическая теория чисел, применяющая методы анализа. Например, с помощью теории комплексного переменного в конце XIX века был доказан асимптотический закон распределения простых чисел.

       В отдельный раздел теории чисел могут выделяться задачи, предметом которых являются диофантовы приближения (алгебраических и трансцендентных чисел рациональными числами), теорию трансцендентных чисел, геометрическую теорию чисел.

      Арифметика получает основу с развитием счёта, решением конкретных практических задач и появлением понятия натурального числа. В «Началах» Евклида изучается делимость чисел, вводится понимание простых чисел. Древнегреческий процесс получения последовательности простых — решето Эратосфена.

       Как математическая дисциплина теория чисел восходит к трудам древнегреческого математика Диофанта Александрийского, в которых изучались задачи решения алгебраических уравнений в целых и рациональных числах.

     В 850 году арабский астроном и математик Сабит ибн Курра предложил формулу для нахождения некоторых пар дружественных чисел.

      В Европе до XVII века рассматривались отдельные задачи теоретико-числовой направленности. Исследованы числа Фибоначчи (1202 год). Были переведены и прокомментированы работы Диофанта.

       В XVII веке ряд теоретико-числовых проблем был поставлен и решён французским математиком Пьером Ферма, которого можно считать основателем современной теории чисел. Его авторству принадлежит «метод бесконечного спуска» для доказательства свойств натуральных чисел, малая теорема Ферма, теорема Ферма о многоугольных числах: каждое натуральное число можно представить не более чем n n-угольными числами. Многочисленные результаты в теории чисел были получены в работах Леонарда Эйлера (1707—1783), который стал применять для решения теоретико-числовых проблем методы математического анализа. Гипотеза Гольдбаха—Эйлера поныне не доказана.

     После Эйлера работы по теории чисел встречаются у ряда западных математиков XVII—XIX веков, его исследования были продолжены Лагранжем и Лежандром.

      Карл Фридрих Гаусс в Disquisitiones Arithmeticae излагает теорию сравнений в современной нотации, решает сравнения произвольного порядка, исследует квадратичные формы; комплексные корни из единицы используются для построения правильных n-угольников, излагаются свойства квадратичных вычетов, приведено гауссово доказательство квадратичного закона взаимности. Гаусс поставил проблему нахождения «высших законов взаимности», которая стимулировала развитие алгебраической теории чисел в XIX—XX веках.

       Разнообразные проблемы теории чисел рассматриваются в работах математиков XIX века: Эйзенштейна, Римана, Дирихле, Куммера, Чебышёва, Лиувилля, Эрмита, Кронекера, Золотарёва. Доказан сформулированный Чебышёвым асимптотический закон распределения простых чисел. Сформулирована не доказанная поныне гипотеза Римана о нулях дзета-функции, утверждающая, что все нетривиальные корни уравнения ζ(s)=0 лежат на так называемой критической прямой Res=12.

Среди российских математиков XIX века выделяют труды Чебышёва, Коркина, Золотарёва, Вороного.

      В XX веке в работах Гильберта, Такаги, Фуртвенглера, Хассе и Артина была построена теория полей классов, находящая применение в алгебраической теории чисел. Продолжилось развитие методов комплексного переменного в теории чисел. Математик А. О. Гельфонд в 1934 году решил Седьмую проблему Гильберта о трансцендентности чисел вида

α^β, где α,β — алгебраические числа. Вопросы приближения алгебраических чисел рациональными были развиты в работах А. Туэ, К. Зигеля и Ф. Рота. Это позволило доказать конечность числа представлений натуральных чисел неприводимыми бинарными формами степени выше 2.

И.М. Виноградов с помощью развитого им метода тригонометрических сумм доказал одну из двух проблем Гольдбаха, поставленную в XVIII веке: все нечетные числа, начиная с некоторого, могут быть представлены в виде суммы трёх простых чисел.

     В 1970 году Юрий Матиясевич доказал алгоритмическую неразрешимость проблемы нахождения произвольных алгебраических диофантовых уравнений, решив Десятую проблему Гильберта.

       Геометрическая теория чисел изучает в основном «пространственные решётки» — системы точек с целочисленными координатами (в прямоугольной или косоугольной системе координат). Эти конструкции имеют большое значение для геометрии и для кристаллографии, их исследование тесно связано с арифметической теорией квадратичных форм и с другими важными разделами теории чисел. Основателем геометрической теории чисел стал Герман Минковский.

        Теория чисел вплоть до XX века считалась чистой наукой, не имеющей практического применения. Такой её называл, в частности, английский математик Харди. Начиная со второй половины XX века появились криптографические протоколы, полагающиеся на вычислительную трудность решения задачи разложения (факторизации) больших чисел на простые, трудность решения задачи дискретного логарифмирования и других теоретико-числовых задач. Причисление таким задачам некоей вычислительной сложности не имеет, само по себе, простого математического рецепта и является скорее предметом веры, что не мешает использовать соответствующие криптографические протоколы, например, в банковской практике.

• Элементарная теория чисел – раздел теории чисел, изучающий свойства чисел элементарными методами. Такие методы включают использование свойств делимости, различных форм аксиомы индукции и комбинаторные соображения. Иногда понятие элементарных методов расширяют за счёт привлечения простейших элементов математического анализа. Традиционно неэлементарными считают доказательства, в которых используются мнимые числа.

    К элементарной теория чисел обычно относят задачи, возникающие в таких разделах теории чисел, как теория делимости, теория сравнений, теоретико-числовые функции, неопределённые уравнения, разбиения на слагаемые, аддитивные представления, приближения рациональными числами, цепные дроби. Нередко решение таких задач приводит к необходимости выходить за рамки элементарных методов.

       Иногда вслед за отысканием неэлементарного решения какой-нибудь задачи находят и её элементарное решение.

       Задачи элементарной теория чисел имеют, как правило, многовековую историю и нередко стоят в истоках современных направлений теории чисел и алгебры.

       Из сохранившихся клинописных таблиц древних вавилонян можно сделать вывод, что им не были чужды задачи разложения натуральных чисел на простые множители. В V в. до н. э. пифагорейцы построили учение о чётных и нечётных числах и обосновали предложение: произведение двух натуральных чисел чётно тогда и только тогда, когда хотя бы один из сомножителей - чётное число. Общая теория делимости, по существу, была построена Евклидом в его «Началах».

       В элементарной теории чисел числа изучаются без использования других разделов математики. Делимость чисел – одно из основных понятий арифметики, связанное с операцией деления.

      С точки зрения теории множеств, делимость целых чисел является отношением, определенным на множестве целых чисел. Если для некоторого целого числа a и целого числа b существует такое целое число q, что bq=a, то говорят, что число a делится нацело на b или что b делит a. При этом число b называется делителем числа a, делимое a будет кратным числа b, а число q называется частным от деления a на b. Хотя свойство делимости определено на всём множестве целых чисел, обычно рассматривается лишь делимость натуральных чисел. В частности, функция количества делителей натурального числа подсчитывает лишь его положительные делители.

       Основная теорема арифметики: Каждое натуральное число n>1 можно представить в виде

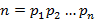
, где множители – степени простых чисел, причём такое представление единственно, если не учитывать порядок следования множителей.

       С начала нашей эры на основе работ александрийских математиков начинается бурное развитие идеалистической философии: снова возрождаются идеи Платона и Пифагора, и эта философия неоплатоников и неопифагорейцев быстро снижает научное значение работ новых представителей математической мысли. Математическая мысль не замирает, а время от времени проявляется в работах отдельных математиков, таких как Диофант.

       Развитию алгебры препятствовало то, что ещё недостаточно вошли в употребление символические записи, намёк на которые впервые встречается в трудах Диофанта, пользовавшегося лишь отдельными символами и сокращениями записи.

• Диофант (Diophantus) – греческий математик, прозванный в Средние века «отцом алгебры». Он представляет одну из наиболее трудных загадок в истории науки. Не известны ни время, когда он жил, ни предшественники его, которые работали бы в той же области. Промежуток времени, когда мог жить Диофант, составляет полтысячелетия! Нижняя грань этого про межутка определяется без труда: в своей книге о многоугольных числах Диофант неоднократно упоминает математика Гипсикла Александрийского, который жил в середине II века до н.э. С другой стороны, в комментариях Теона Александрийского к «Альмагесту» знаменитого астронома Птолемея помещён отрывок из сочинения Диофанта. Теон жил в середине IV века н.э. Этим определяется верхняя грань этого промежутка. Итак, 500 лет!
  

Французский историк науки Поль Таннери, издатель наиболее полного текста Диофанта, попытался сузить этот промежуток. В библиотеке Эскуриала он нашёл отрывки из письма Михаила Пселла, византийского учёного XI века, где говорится, что «учёнейший Анатолий, после того как собрал наиболее существенные части этой науки (речь идёт о введении степеней неизвестного и об их обозначениях), посвятил их своему другу Диофанту». Анатолий Александрийский действительно составил «Введение в арифметику», отрывки из которой приводят в дошедших до нас сочинениях Ямблих и Евсевий. Но Анатолий жил в Александрии в середине III века н.э. и даже более точно - до 270 года, когда он стал епископом Лаодакийским. Значит, его дружба с Диофантом, которого все называют Александрийским, должна была иметь место до этого. Итак, если знаменитый александрийский математик и друг Анатолия по имени Диофант составляют одно лицо, то время жизни Диофанта - середина III века н.э.

       Сама же «Арифметика» Диофанта посвящена «достопочтенному Дионисию», который, как видно из текста «Введения», интересовался арифметикой и её преподаванием. Хотя имя Дионисий было в то время довольно распространённым, Таннери предположил, что «достопочтенного» Дионисия следует искать среди известных людей эпохи, занимавших видные посты. И вот оказалось, что в 247 году епископом Александрии стал некий Дионисий, который с 231 года руководил христианской гимназией города! Поэтому Таннери отождествил этого Дионисия с тем, которому посвятил свой труд Диофант, и пришёл к выводу, что Диофант жил в середине III века н.э. Мы можем, за неимением лучшего, принять эту дату.

       А вот место жительства Диофанта хорошо известно - это знаменитая Александрия, центр научной мысли эллинистического мира.

        После распада огромной империи Александра Македонского Египет в конце IV века до н.э. достался его полководцу Птолемею Лагу, который перенёс столицу в новый город - Александрию. Вскоре этот многоязыкий торговый город сделался одним из прекраснейших городов древности. Размерами его превзошёл впоследствии Рим, но долгое время ему не было равного. И вот именно этот город стал на многие века научным и культурным центром древнего мира. Это было связано с тем, что Птолемей Лаг основал Музейон, храм Муз, нечто вроде первой Академии наук, куда приглашались наиболее крупные учёные, причём им назначалось содержание, так что основным делом их были размышления и беседы с учениками. При Музейоне была построена знаменитая библиотека, которая в лучшие свои дни насчитывала более 700 000 рукописей. Неудивительно, что учёные и жаждущие знаний юноши со всего мира устремились в Александрию, чтобы послушать знаменитых философов, поучиться астрономии и математике, иметь возможность в прохладных залах библиотеки углубиться в изучение уникальных рукописей.

        Музейон пережил династию Птолемеев. В первые века до н.э. он пришёл во временный упадок, связанный с общим упадком дома Птолемеев в связи с римскими завоеваниями (Александрия была окончательно завоевана в 31 году до н.э.), но затем в первые века н.э. он снова возродился, поддерживаемый уже римскими императорами.

       Александрия продолжала оставаться научным центром мира. Рим никогда не был в этом отношении её соперником: римской естественной науки просто не существовало.

       И если в III-II веках до н.э. Музейон блистал именами Евклида, Аполлония, Эратосфена, Гиппарха, то в I-III веках н.э. здесь работали такие учёные как Герон, Птолемей и Диофант.

Чтобы исчерпать всё известное о личности Диофанта, приведём дошедшее до нас стихотворение-загадку:

Прах Диофанта гробница покоит; дивись ей и камень

Мудрым искусством его скажет усопшего век.

Волей богов шестую часть жизни он прожил ребенком.

И половину шестой встретил с пушком на щеках.

Только минула седьмая, с подругой он обручился.

С нею, пять лет проведя, сына дождался мудрец;

Только полжизни отцовской возлюбленный сын его прожил.

Отнят он был у отца ранней могилой своей.

Дважды два года родитель оплакивал тяжкое горе,

Тут и увидел предел жизни печальной своей.

      Используя современные методы решения уравнений можно сосчитать, сколько лет прожил Диофант. Составим уравнение:

х/6 + х/12 + х/7 + 5 + х/2 + 4 = х.

Решением этого уравнения является число 84. Таким образом, Диофант прожил 84 года.

      Однако для этого вовсе не нужно владеть искусством Диофанта! Достаточно уметь решать уравнение 1-й степени с одним неизвестным, а это умели делать египетские писцы ещё за 2 тысячи лет до н.э.

        Диофант нередко упоминается как «отец алгебры». Он – автор «Арифметики», книги, посвящённой нахождению положительных рациональных решений неопределённых уравнений. В наше время под «диофантовыми уравнениями» обычно понимают уравнения с целыми коэффициентами, решения которых требуется найти среди целых чисел.

       Диофант был первым греческим математиком, который рассматривал дроби наравне с другими числами. Диофант также первым среди античных учёных предложил развитую математическую символику, которая позволяла формулировать полученные им результаты в достаточно компактном виде.

       В честь Диофанта назван кратер на видимой стороне Луны.

     Основное произведение Диофанта – «Арифметика». К сожалению, сохранились только 6 первых книг из 13.

       В классической греческой математике, которая нашла своё завершение в «Началах» Евклида, под числом άριJμός - «аритмос » или «арифмос »; (отсюда название «арифметика» для науки о числах) понималось множество единиц, т.е. целое число. Ни дроби, ни иррациональности числами не назывались. Строго говоря, никаких дробей в «Началах» нет. Единица считается неделимой и вместо долей единицы рассматриваются отношения целых чисел; иррациональности появляются как отношения несоизмеримых отрезков, например, число, которое мы теперь обозначаем √2, для греков классической эпохи было отношением диагонали квадрата к его стороне. Об отрицательных числах не было и речи. Для них не существовало даже никаких эквивалентов.

        Совершенно иную картину мы находим у Диофанта. Он приводит традиционное определение числа как множества единиц, однако в дальнейшем ищет для своих задач положительные рациональные решения, причём называет каждое такое решение числом (άριJμός - «аритмос»).

       Но этим дело не ограничивается. Диофант вводит отрицательные числа: он называет их специальным термином λει̃ψις - «лейпсис » - производное от глагола λει̃πω - «лейпо », что означает недоставать, нехватать, так что сам термин можно было бы перевести словом «недостаток». Положительное число Диофант называет словом ΰπαρξις - «ипарксис », что означает существование, бытие, а во множественном числе это слово может означать имущество или достояние. Таким образом, терминология Диофанта для относительных чисел близка к той, которую употребляли в Средние века на Востоке и в Европе. Скорее всего, это было просто переводом с греческого на арабский, санскрит, латынь, а затем на различные языки Европы.

             «Арифметика» Диофанта – это сборник задач (их всего 189), каждая из которых снабжена решением (или несколькими способами решения) и необходимыми пояснениями. Поэтому, с первого взгляда, кажется, что она не является теоретическим произведением. Однако, при внимательном чтении видно, что задачи тщательно подобраны и служат для иллюстрации вполне определенных, строго продуманных методов. Как это было принято в древности, методы не формулируются в общем виде, а повторяются для решения однотипных задач.

        Диофант формулирует для относительных чисел правило знаков:

«отрицательное, умноженное на отрицательное, даёт положительное, тогда как отрицательное на положительное даёт отрицательное, и отличительный знак для отрицательного есть - перевёрнутая и укороченная (буква) ψ».

        Заметим, что хотя Диофант ищет только рациональные положительные решения, в промежуточных выкладках он пользуется отрицательными числами.

Мы можем, таким образом, отметить, что Диофант расширил числовую область до множества рациональных чисел, в котором можно беспрепятственно производить все четыре действия арифметики.

       Диофантовы уравнения - алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, имеющие число неизвестных, превосходящее число уравнений, и у которых разыскиваются целые или рациональные решения. Диофантовы уравнения имеют, как правило, много решений, поэтому их называют неопределенными уравнениями. Пример такого уравнения: ax + by = 1, где а и b - целые взаимно простые числа (такие, что общими делителями для этих чисел являются лишь + 1 и – 1).

      Сначала Диофант исследует системы уравнений 2-го порядка от 2 неизвестных; он указывает метод нахождения других решений, если одно уже известно. Затем аналогичные методы он применяет к уравнениям высших степеней.

        Наверное, самым известным диофантовым уравнением является

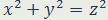
Его решения - пифагоровы тройки: (3; 4; 5), (6; 8; 10), (5; 12; 13), (12; 35; 37)…

       Доказательство неразрешимости в целых числах диофантового уравнения

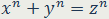
(Великая теорема Ферма) было закончено английским математиком Эндрю Уайлсом в 1994 году.

        Ещё один пример диофантового уравнеия - уравнение Пелля

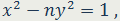
где параметр n не является точным квадратом.

        Большая часть «Арифметики» - это сборник задач с решениями, умело подобранных для иллюстрации общих методов. Главная проблематика - нахождение положительных рациональных решений неопределённых уравнений. Диофант не даёт никаких общих методов решения задач; данные им решения почти не допускают систематизации. В значительной степени это объясняется несовершенством символики Диофанта. В новое время «Арифметика» явилась отправной точкой исследований в области теории чисел (Ферма, Эйлер).

        В X веке «Арифметика» была переведена на арабский язык, после чего математики стран ислама (Абу Камил и др.) продолжили некоторые исследования Диофанта. В Европе интерес к «Арифметике» возрос после того, как Рафаэль Бомбелли обнаружил это сочинение в Ватиканской библиотеке и опубликовал 143 задачи из него в своей Алгебре (1572). В 1621 году появился классический, подробно прокомментированный латинский перевод «Арифметики», выполненный Баше де Мезириаком. Методы Диофанта оказали огромное влияние на Франсуа Виета и Пьера Ферма; впрочем, в Новое время неопределённые уравнения обычно решаются в целых числах, а не в рациональных, как это делал Диофант.

          «Арифметика» стала поворотным пунктом в развитии алгебры и теории чисел. Именно здесь произошёл окончательный отказ от геометрической алгебры.

      В XX веке под именем Диофанта обнаружен арабский текст ещё 4 книг «Арифметики». И. Г. Башмакова и Е. И. Славутин, проанализировав этот текст, выдвинули гипотезу, что их автором был не Диофант, а хорошо разбиравшийся в методах Диофанта комментатор, вероятнее всего — Гипатия.

     Труды Диофанта имели фундаментальное значение для развития алгебры и теории чисел. С именем этого учёного связано появление и развитие алгебраической геометрии, проблемами которой впоследствии занимались Леонард Эйлер, Карл Якоби и другие авторы.

       Трактат Диофанта «О многоугольных числах» сохранился не полностью. В сохранившейся части методами геометрической алгебры выводится ряд вспомогательных теорем. Из сочинений Диофанта «Об измерении поверхностей» и «Об умножении» также сохранились лишь отрывки. Книга Диофанта «Поризмы» известна только по нескольким теоремам, используемым в «Арифметике».

        Десятая проблема Гильберта - одна из 23 задач, которые Давид Гильберт предложил 8 августа 1900 года на II Международном конгрессе математиков. В докладе Гильберта постановка десятой задачи самая короткая из всех: «Пусть задано диофантово уравнение с произвольными неизвестными и целыми рациональными числовыми коэффициентами. Указать способ, при помощи которого возможно после конечного числа операций установить, разрешимо ли это уравнение в целых рациональных числах.»

       Доказательство алгоритмической неразрешимости этой задачи заняло около двадцати лет и было завершено Юрием Матиясевичем в 1970 году.

       Во многом благодаря деятельности Паппа Александрийского (III век) до нас дошли сведения об античных учёных и их трудах. После Аполлония (со II века до н. э.) в античной науке начался спад. Новых глубоких идей не появляется. В 146 году до н. э. Рим захватывает Грецию, а в 31 году до н. э. - Александрию. На фоне общего застоя и упадка резко выделяется гигантская фигура Диофанта Александрийского - последнего из великих античных математиков, «отца алгебры».

      Имя Диофанта носят следующие математические объекты:

диофантов анализ,

диофантовы приближения,

диофантовы уравнения.