Из истории теории чисел (Окончание)

Баше де Мезириак, Клод Гаспар (Claude Gaspard Bachet de Méziriac) (В некоторых русских источниках называется Мезирьяк) — французский математик, поэт, лингвист, переводчик. Родился 9 октября 1581 года в Бурк-ан-Брес, Франция, в состоятельной дворянской семье. Рано лишился обоих родителей.
Учился в Реймсе в иезуитском коллеже у Жака де Билли, с которым его связала тесная дружба и общий интерес к математике. Изучил несколько языков, в том числе латинский, греческий, иврит, итальянский и испанский. Писал стихи на французском, итальянском и латыни.
Преподавал в иезуитском колледже в Милане, прежде чем отказался от своего обета и посвятил себя переводу латинских поэтов и греческих математиков. Женился в 1612 году, стал отцом семерых детей.
В этом же 1612 году Баше опубликовал сборник занимательных арифметических задач «Problèmes plaisants» (2-е дополненное издание вышло в 1624 году). Огромный интерес вызвала публикация им в 1621 году «Арифметики» Диофанта на греческом и в собственноручном переводе на латинский, с обширными комментариями. Этот перевод стал настольной книгой и источником новых открытий для Пьера Ферма и других выдающихся математиков XVII века; именно на полях этой книги Ферма записал формулировку своей Великой теоремы.
Среди других достижений Баше по арифметике и теории чисел можно назвать следующие: исследование диофантовых уравнений, для решения которых он разработал ряд оригинальных алгоритмов – в том числе с помощью непрерывных дробей. Первая публикация фундаментальной формулы, называемой сейчас соотношением Безу. Баше дал (в словесной формулировке) ее частный случай для взаимно простых чисел. Описал общий метод составления магических квадратов любого порядка. Высказал предположение о представимости любого натурального числа в виде суммы не более четырех квадратов, доказанное в XVIII в. Лагранжем. Баше опубликовал также антологию французской поэзии под названием «Délices».
Он – один из первых членов Французской академии (1635).
Умер Баше де Мезириак 26 февраля 1638 года (56 лет).
В XVII веке вместе с интересом к точным наукам воскресает и интерес к теории чисел. Особенно он возрос после издания в 1621г. литератором и любителем математики Клодом-Гаспаром Баше де Мезириаком (1581-1638) греческого текста «Арифметики» Диофанта с латинским переводом и комментариями. Во Франции образовалась группа ученых, занимавшихся задачами теории чисел. В неё входили Пьер Ферма, сотрудник монетного двора Бернар Френикль де Бесси (1605-1675), лионский учитель математики Жак де Билли (1602-1679),Мерсенн, отчасти Декарт и Блез Паскаль. Эти люди жили в разных городах Франции, и некоторые даже никогда не видели друг друга.
Зато они вели оживлённую переписку как непосредственно друг с другом, так и через Мерсенна.
Впоследствии в эту переписку были втянуты учёные Англии – Валллис, Броункер и Голландии – Гюйгенс, Схоотен. Когда Мерсенн скончался, его функции посредника между учёными занял друг Ферма де Каркави, любитель математики и королевский библиотекарь, один из организаторов Парижской академии наук.
Однако из всей этой плеяды учёных одному только Пьеру Ферма удалось выделить из хаоса многочисленных задач и частных вопросов, сразу же возникающих перед исследователем при изучении свойств целых чисел, те основные проблемы, которые стали центральными для всей классической теории чисел. Ему же принадлежит открытие замечательного метода для доказательства теоретико-числовых предложений – так называемого метода бесконечного спуска.Поэтому Ферма по праву может считаться основоположником алгебраической теории чисел.

Уроженец юга Франции, Пьер Ферма (Pierre de Fermat) (1601-1665) провёл большую часть жизни в Тулузе, где состоял советником местного парламента (высшего суда). Он получил юридическое образование, был прекрасным знатоком древних и современных ему языков: латыни, древнегреческого, испанского, итальянского, писал изящные стихи по-французски, по-испански и по-латыни.
Греческий он знал настолько хорошо, что делал поправки ко многим учебным переводами мог бы прославиться как знаток эллинизма. Изучение в подлинниках Евклида, Архимеда, Апполония, Паппа и Диофанта, вероятно, послужило толчком для занятий Ферма математикой. Именно здесь и проявился с полной силой его гений.
Ферма был чрезвычайно разносторонним математиком: он существенно развил методы определения площадей и объёмов, создал новый метод касательных и экстремумов, наряду с Декартом явился создателем аналитической геометрии, вместе с Паскалем заложил основы теории вероятностей. Как и большинство учёных того времени, Ферма не ограничивался исследованиями по «чистой» математике. Он занимался оптикой, и ему принадлежит носящий его имя принцип минимума, которому следует луч света при прохождении через неоднородную среду.
Одной из любимых областей математики была для Ферма теория чисел, которой он занялся, по-видимому, в середине 30х годов и которой посвящены наиболее вдохновенные строки его писем. «Арифметика – писал он, – имеет свою собственную область, теорию целых чисел, эта теория была лишь слегка затронута Евклидом и не была достаточно разработана его последователями (если только она не содержалась в тех книгах Диофанта, которых нас лишило разрушительное действие времени); арифметики, следовательно, должны её развивать или возобновить».
Математики Древней Греции со времён Пифагора собирали и доказывали разнообразные утверждения, относящиеся к натуральным числам (например, методы построения всех пифагоровых троек, метод построения совершенных чисел и т. п.). Диофант Александрийский (III век н. э.) в своей «Арифметике» рассматривал многочисленные задачи о решении в рациональных числах алгебраических уравнений с несколькими неизвестными (ныне диофантовыми принято называть уравнения, которые требуется решить в целых числах).
Ферма постоянно интересовался арифметическими задачами, обменивался сложными задачами с современниками. Например, в своём письме, получившем название «Второго вызова математикам» (февраль 1657), он предложил найти общее правило решения уравнения Пелля
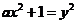
в целых числах. В письме он предлагал найти решения при a=149, 109, 433. Полное решение задачи Ферма было найдено лишь в 1759 году Эйлером.
Ферма писал мало и всегда очень сжато, а кроме того, не публиковал свои работы, циркулировавшие при его жизни лишь в рукописях. Некоторые открытия он изложил только в переписке. Своё намерение написать специальное сочинение по теории чисел он не осуществил. Поэтому результаты Ферма по теории чисел дошли до нас в разрозненном виде: некоторые содержатся в его письмах, другие представляют его замечания к задачам Диофанта на полях принадлежавшего ему экземпляру «Арифметики». Только в 1670 г., после смерти Ферма, его старший сын Самюэль выпустил новое издание Диофанта с комментариями Баше и замечаниями Ферма, а позднее собрал сохранившиеся в бумагах отца математические наброски и небольшие трактаты и издал их под названием «Разные математические сочинения». Но и после этого были найдены многие письма и заметки Ферма, не вошедшие в это издание.
Начал Ферма с задач про магические квадраты и кубы, но постепенно переключился на закономерности натуральных чисел — арифметические теоремы. Таким образом, теоретико - числовые результаты Ферма дошли до последующих математиков в виде проблем, в подавляющем большинстве
случаев без доказательств и указаний на внутренние связи между ними. После смерти Ферма проблемы эти пролежали без движения около семидесяти лет пока ими не заинтересовался Л. Эйлер. С этого момента началась их новая жизнь. Исследования Эйлера превратили теорию чисел в неотъемлемую составную часть математики.
Занимаясь арифметикой целых чисел, Ферма обратил внимание на большую роль, которую играют простые числа. По-видимому, он начал искать различные критерии для определения того, будет ли заданное число N простым или составным. Он искал также выражения F(n), которые при любом целом значении n давали бы только простые числа.
Ферма изучал числа вида
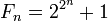
и выдвинул гипотезу, что все они простые. Однако, эта гипотеза была опровергнута Эйлером в 1732 году, нашедшим разложение числа F5 на простые делители:
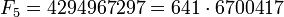
.
Простые числа указанного вида называются теперь простыми числами Ферма. До сих пор неизвестно, существует ли конечное число простых чисел Ферма или их бесконечно много.

Позже Хр. Гольдбах и Л. Эйлер доказали. что не существует целого многочлена P(x) c целыми коэффициентами, все значения которого при целых x были бы простыми числами.
Одним из критериев для определения простоты числа послужила так называемая малая теорема Ферма: если p – это простое число, a – целое число, не делящееся на p, то ap-1 – 1 делится на p. Формально пишется так:
ap-1 ≡ 1 (mod p).
Ферма сформулировал это предложении сначала для a = 2, затем для любого a. Он высказал теорему без доказательства, первое доказательство дали Леонард Эйлер и Готфрид Вильгельм Лейбниц.
Малая теорема Ферма является частным случаем теоремы Эйлера, которая, в свою очередь, является частным случаем теоремы Кармайкла и теоремы Лагранжа для конечных циклических групп.
В малой теореме на частном примере установлено одно из основных предложений теории конечных групп: порядок любого элемента конечной группы является делителем порядка группы.

Великая теорема Ферма (или Последняя теорема Ферма) — одна из самых популярных теорем математики. Ферма указал, что «Невозможно разложить куб на два куба, или биквадрат на два биквадрата, или вообще степень, большую двух, на две степени с тем же самым показателем.» Условие формулируется просто, на «школьном» арифметическом уровне, однако доказательство теоремы искали многие математики более трёхсот лет. Современная формулировка теоремы:
«Уравнение xn + yn = zn (где n – целое число большее двух) не имеет решений в целых положительных числах».
Теорема была доказана в 1994 году Эндрю Уайлсом с коллегами (доказательство опубликовано в 1995 году). В 2016 году за доказательство Великой теоремы Ферма Эндрю Уайлс получил Абелевскую премию.
В общем виде теорема была сформулирована Пьером Ферма в 1637 году на полях «Арифметики» Диофанта. Дело в том, что Ферма делал свои пометки на полях читаемых математических трактатов и там же формулировал пришедшие на ум задачи и теоремы. Теорему, о которой ведётся речь, он записал с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было поместить на полях книги.
Эйлер в 1770 году доказал теорему для случая n = 3, Дирихле и Лежандр в 1825 — для n = 5, Ламе — для n = 7. Куммер показал, что теорема
верна для всех простых n, меньших 100, за возможным исключением так называемых иррегулярных простых 37, 59, 67.
Над полным доказательством Великой теоремы работало немало выдающихся математиков и множество дилетантов-любителей; считается, что теорема стоит на первом месте по количеству некорректных «доказательств». Тем не менее эти усилия привели к получению многих важных результатов современной теории чисел.

Давид Гильберт в своём докладе «Математические проблемы» на II Международном конгрессе математиков (1900) отметил, что поиск доказательства для этой, казалось бы, малозначимой теоремы привёл к глубоким результатам в теории чисел.
В 1908 году немецкий любитель математики Вольфскель завещал 100 тыс. немецких марок тому, кто докажет теорему Ферма. Однако после Первой мировой войны премия обесценилась.
Упомянем ещё утверждение о представимости любого целого положительного числа суммой не более четырех целых квадратов, впервые вы сказанное Баше де Мезириаком в комментариях к его изданию «Арифметики» Диофанта 1621 г. В замечании, относящемяс к этому месту, Ферма высказал более общую теорему, согласно которой любое натуральное число есть либо n- угольное, либо сумма не более чем n n- угольных чисел, причём утверждал, что располагает её доказательством. В 1636 г теорема стала известной в кругу французских математиков.
Доказательство своё Ферма не сообщил; он лишь упомянул в одном письме 1654 г Паскалю, что вывод опирается на представимость простых чисел вида 4n+1 суммой двух квадратов. Эта теорема Ферма для n=4 была доказана во второй половине 18 века благодаря совместным усилиям Эйлера и Лагранжа, для n=3 – Гауссом (1801) и в общем случае – О. Коши (1813-1815).

Баше де Мезириаку и Ферма принадлежит заслуга постановки задачи о решении неопределенных уравнений в целых числах. До них, следуя за Диофантом, европейские математики обычно искали рациональные решения таких уравнений.
Баше де Мезириак, не зная о своих индийских предшественниках, подробно разработал и изложил на числовых примерах способ решения в целых
положительных числах линейного уравнения с двумя неизвестными ax + by = c, где (a,b)=1. Этот вопрос Баше изложил в замечательном сборнике «Приятных и занимательных задач, рассматриваемых в числах», неоднократно переиздававшихся вплоть до наших дней, - в последний раз книга вышла в 1959 г.
Ферма исследовал гораздо более трудную задачу решения в целых положительных числах уравнения с двумя неизвестными второй степени.
Эйлер доказал (1749) ещё одну гипотезу Ферма (сам Ферма редко приводил доказательства своих утверждений): простые числа вида 4k+1 представляются в виде суммы двух квадратов (5=4+1; 13=9+4), причём единственным способом, а для чисел, содержащих в своём разложении на простые множители простые числа вида 4k+3 в нечётной степени, такое представление невозможно. Эйлеру это доказательство стоило 7 лет трудов; сам Ферма доказывал эту теорему косвенно, изобретённым им индуктивным «методом бесконечного спуска». Этот метод был опубликован только в 1879 году; впрочем, Эйлер восстановил суть метода по нескольким замечаниям в письмах Ферма и неоднократно успешно его применял. Позже усовершенствованную версию метода применяли Пуанкаре и Андре Вейль.
Ферма разработал способ систематического нахождения всех делителей числа, сформулировал теорему о возможности представления произвольного числа суммой не более четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов). Большой интерес вызывали у Ферма фигурные числа. В 1637 году он сформулировал так называемую «золотую теорему»:
Всякое натуральное число — либо треугольное, либо сумма двух или трёх треугольных чисел.
Всякое натуральное число — либо квадратное, либо сумма двух, трёх или четырёх квадратных чисел (Теорема Лагранжа о сумме четырёх квадратов).
Всякое натуральное число — либо пятиугольное, либо сумма от двух до пяти пятиугольных чисел.
И т. д.
Этой теоремой занимались многие выдающиеся математики, полное доказательство сумел дать Коши в 1813 году.
Многие остроумные методы, применяемые Ферма, остались неизвестными. Однажды Мерсенн попросил Ферма выяснить, является ли многозначное число 100 895 598 169 простым. Ферма не замедлил сообщить, что 100 895 598 169 = 898423 х 112303 (оба сомножителя — простые числа); он не пояснил, как нашёл эти делители. В одном из писем Френиклю де Бесси Ферма поставил задачу: найти прямоугольный треугольник, у которого гипотенуза и сумма катетов — квадратные числа (то есть точные квадраты). Френикль высказал сомнение, что задача имеет решение, однако Ферма в ответном письме привёл одно из решений:
Гипотенуза: 4687298610289 = (2165017)^2
Катеты: 4 565 486 027 761 и 1 061 652 293 520;
Сумма катетов: 5627138321281 = (2372153)^2.
Арифметические открытия Ферма опередили время и были забыты на 70 лет, пока ими не заинтересовался Эйлер, опубликовавший систематическую теорию чисел. Одна из причин этого — интересы большинства математиков переключились на математический анализ; сказалось, вероятно, и то, что Ферма использовал устаревшую и громоздкую математическую символику Виета вместо гораздо более удобных обозначений Декарта.
В аналитической теории чисел для вывода и доказательства утверждений о числах и числовых функциях используется мощный аппарат математического анализа (как вещественного, так и комплексного), иногда также теория дифференциальных уравнений. Это позволило значительно расширить тематику исследований теории чисел. В частности, в неё вошли следующие новые разделы:
Распределение простых чисел в натуральном ряду и в других последовательностях (например, среди значений заданного многочлена).
Представление натуральных чисел в виде сумм слагаемых определённого вида (простых чисел, квадратов и т. д.).
Диофантовы приближения.
Первым шагом в применении аналитических методов в теории чисел стал метод производящих функций, сформулированный Эйлером. Для определения количества целочисленных неотрицательных решений линейного уравнения вида
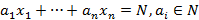
В алгебраической теории чисел понятие целого числа расширяется, в качестве алгебраических чисел рассматривают корни многочленов с рациональными коэффициентами. Была разработана общая теория алгебраических и трансцендентных чисел. При этом аналогом целых чисел выступают целые алгебраические числа, то есть корни унитарных многочленов с целыми коэффициентами. В отличие от целых чисел, в кольце целых алгебраических чисел не обязательно выполняется свойство факториальности, то есть единственности разложения на простые множители.
Вся последующая алгебраическая теория чисел вплоть до работ Гаусса развивалась, отправляясь от проблем Ферма. Исследовались в основном вопросы представления чисел квадратичными формами и задачами диофантова анализа, в частности неопределенные уравнения второго порядка.
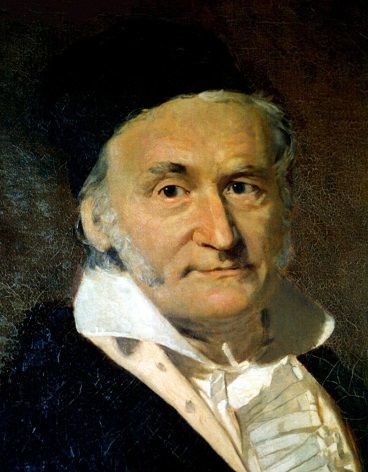
Гаусс открыл кольцо целых комплексных гауссовых чисел, создал для них теорию делимости и с их помощью решил немало алгебраических проблем. Указал знакомую теперь всем геометрическую модель комплексных чисел и действий с ними. Дал классическую теорию сравнений, открыл конечное поле вычетов по простому модулю, глубоко проник в свойства вычетов.
В работах Лагранжа, а особенно Гаусса, первый из названных вопросов был преобразован в теорию квадратичных форм, которая по существу являлась первым учением об арифметике квадратичных полей. Этот же вопрос привёл Эйлера к открытию квадратичного закона взаимности.
Наконец, в XIX веке исследования, связанные с великой теоремолй Ферма и законами взаимности, потребовали расширения области арифметики. При изучении биквадратичного закона взаимности Гаусс ввёл целые комплексные числа, а попытки доказательства великой теоремы привели к рассмотрению целых чисел в полях деления круга.
Центральной проблемой алгебраической теории чисел в XIX веке становится построение арифметики в кольцах алгебраических чисел. Для спасения обычных законов арифметики вводятся идеальные множители (Куммер, Золотарев), идеалы (Дедекинд) и дивизоры (Кронекер). Строится теория колец, модулей и идеалов, появляются локальные и полулокальные кольца. И все эти ветви восходят к проблемам Ферма.

Э. Куммер ввёл понятие класса идеальных чисел. Два идеальных числа принадлежат одному классу, если их отношение лежит в первоначальном поле k. Он получил важный результат: число этих классов h конечно, и они образуют абелеву группу по умножению. Таким образом, любое идеальное число можно считать корнем h-й степени из некоторого числа первоначального поля k. Число классов h явно выписывается через константы поля (регулятор, дискриминант, степень поля).
В дальнейшем понятие идеального числа было заменено эквивалентным понятием идеала, которое удается описать средствами самого поля k, и уже в середине ХХ века идеал уступил место более емкому понятию дивизор. Поэтому современная теория Куммера излагается на языке дивизоров. Но для полей алгебраических чисел классическое понятие идеала совпадает с понятием дивизора. Понятие идеала тесно связано с понятием неассоциированных чисел, что способствует пониманию глубоких связей теории Куммера и теории единиц Дирихле. Хотя Э. Куммеру и не удалось решить проблему Ферма, но его идеи вышли далеко за рамки этой задачи, и понятие идеала ныне является одним из главных для всей математики.

К Д. Гильберту восходит совершенно новая точка зрения на теорию полей классов, которая сохранилась до настоящего времени. Он понял, что между всеми относительно абелевыми расширениями поля k и всеми полями классов для этого поля должно существовать взаимно однозначное соответствие.
Следующий важный этап в развитии теории полей классов связан с именем Э. Артина, выявившего особую роль канонического изоморфизма между группой Галуа и группой классов идеалов.
